Inscription / Connexion Nouveau Sujet
Fonctions
Bonjour ! J'aurais besoin d'aide pour un exercice de mathématiques sur les fonctions.
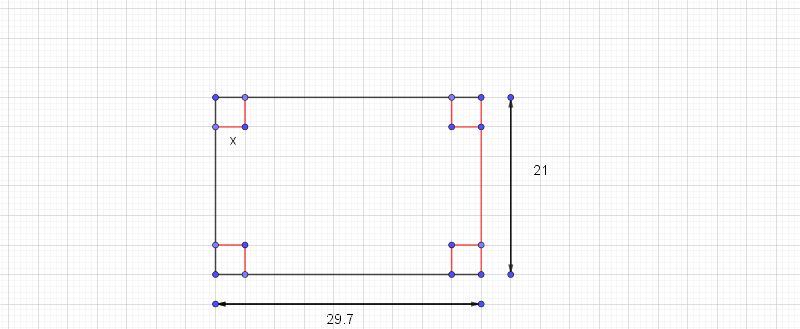
Chloé veut construire une boîte sans couvercle. Pour cela, elle découpe des carrés identiques dans les coins d'une feuille de papier de format A4 (21 cm de largeur et 29,7 cm de longueur.
L'objectif est de déterminer la mesure des côtés des carrés pour que la boîte ait un volume maximal. On note x la longueur des côtés des carrés.
Sans justification, donner la valeur minimale et la valeur maximale que peut prendre x.
Merci d'avance de votre aide !
quand tu replies les côtés (rouges) pour former la boîte.
Quelle sera sa largeur ?....
sa profondeur ?.....
sa hauteur ?......
Au lieu d'écrire profondeur, je vais "dire" largeur (l) de la boîte après pliage
Quelle est sa largeur (l)
et
quelle est sa longueur ?
Alors bien sûr , en troisième , point facile de trouver les valeurs minimale et maximale
tu dois les donner
"Sans justification, donner la valeur minimale et la valeur maximale que peut prendre x. "
=( 21 - 2x) ( 29,7 - 2x) x
= x ( 21*29,7 - 21* (-2x) -2x * 29,7 -2x*(-2x)
= x ( 623,7+ 42x -59,4x +4x2
= 623,7x + 42x2 - 59,4x2 + 4x3
623,7x - 42x² - 59,4x²+ 4x3
bon ça pour le calcul.
reste :
"Sans justification, donner la valeur minimale et la valeur maximale que peut prendre x. "
Bonjour à vous deux
Voir ici un problème similaire
![]() DM n°3
DM n°3
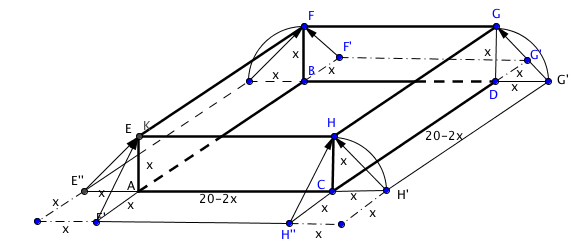
et la figure en perspective d'un autre problème similaire
ici V(x)=x(29,7-2x)(21-2x)
V(x)=x(29,7*21-2x*29,7-2x*21-2x*(-2x))=x(627,3-59,4x-42x+4x2)
V(x)=4x3-101,4x2+627,3
pour trouver (approximativement) le volume maxi de la boîte au niveau 3 ème, se servir de l'équation ci-dessus pour tracer par points la courbe représentative et déterminer entre quelles valeurs peut se situer le maximum, puis affiner en prenant des valeurs de x comprises dans l'encadrement.
Panda54
Il serait bon de dire la valeur maximale et minimale de quoi
pour x, ses valeurs possibles sont comprises entre 0 et 21/2, ces 2 valeurs étant exclues car la boîte n'existerait plus. Si x=0 plus de découpe donc profondeur nulle et si x=10,5 la largeur est nulle
donc 0<x<10,5
pour le volume maxi voir ici
[url]https://www.ilemaths.net/sujet-dm-volume-maximum-d-une-boite-681185.html
[/url]