Inscription / Connexion Nouveau Sujet
Fonctions
Bonjour, j'ai cet exercice à faire mais j'ai quelques difficultés sur la question 2. J'ai commencé mes recherches et j'aimerais savoir si c'est juste. Merci d'avance !
On considère une fonction f définie et dérivable sur [0;+ [ dont on donne la représentation graphique.
[ dont on donne la représentation graphique.
Les coordonnées des points indiqués sont A (0;1), D(2;4) et C(2;3). La droite (AD) est tangente à la courbe au point d'abscisse 0.
La courbe rencontre l'axe des abscisses au point d'abscisse 4.
On sait aussi que f(6) = 1 et que la tangente au point d'abscisse 6 passe par le point E (3; 0). 1.
1.Par lecture graphique :
a. déterminer f (0), f' (0) et f' (6)
b. déterminer une équation de la tangente à la courbe au point d'abscisse 6
c. dresser le tableau de signes de f.
a. Par lecture graphique, je peux déterminer que
f(0)=1
f'(0)=3/2=1,5
f'(6)=1/3
b. y=f'(a)(x-a)+f(a) où f(a)=1 et f'(a)=1/3.
y=1/3(x-6)+1
y=(1/3)x-1
c. x 0 2 4 +
f' + 0 - 0 +
2.On considère la fonction g définie par g = 1/f.
a. Déterminer le domaine de définition de g.
b. Donner l'expression de g' à l'aide de f et de f'.
a. g est défini sur [0;+ [
[
b. g(x)=1/f donc g(x)=1/v où v=f et v'=f'
g'(x)=-v'/v2
g'(x)=-f/f2
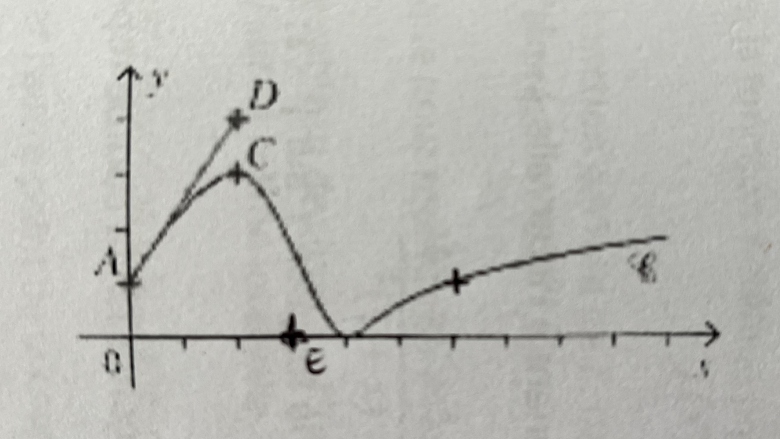
Bonjour
D'accord pour f(0) f'(0) f'(6)
l'équation de la tangente en 6
Vous donnez le signe de on veut celui de
.
Il n'y a que le a) à revoir
b) on a bien
et
sont des fonctions
et
sont des nombres réels
on a l'égalité qu'entre éléments de même ensemble.
D'accord, j'ai continué de chercher pour le a) et voici ce que j'ai trouvé.
Il faut exclure les valeurs où f(x)=0 et on peut voir sur le graphique que f(4)=0.
donc g est définie sur [0;4[U]4;+ [
[


