Inscription / Connexion Nouveau Sujet
fonctions associées
Bonjour, j'ai un DM a rendre lundi et j'ai une partie d'un exercice ou je ne suis pas sur de ce que j'ai fait, Merci de bien vouloir m'aider.
l'exercice est sur les fonctions associées. il y a une représentation graphique mais je ne sais pas comment la refaire ici. on nous demande de faire le tableau de variation de la fonction f. Ensuite nous devons faire le tableau pour
g(x)=f(x)-3 j'ai trouvé le même tableau de variation, seules les valeurs de g(x) changent.
h(x)= -2f(x) ici f et h ont des sens de variation contraires
et enfin k(x) = 1/f(x) et c'est là où j'ai des doutes.
Tabeau de variation de f:
f(x) est croissante sur [1;3] et décroissante sur [-3;-1]
[3;4]
Tableau de variation de k:
k(x) est de la forme 1/u(x) définie par u(x)
0, avec u(x)=f(x).
les fonctions k et f ont des sens de variation contraires.
sur [-3;-1][3;4] f(x) est décroissante, don k(x) est croissante.
sur [-1;3] f(x) est croissante donc k(x) est décroissante.
dans la fonction k(x) comme f(x) est au dénominateur il doit y avoir au moins une valeur interdite et là je bloque.
Merci d'avance de votre aide
bonjour
tes réponses concernant les changements (ou pas) de variation sont justes :
ajouter une constante conserve le sens de variation.
multiplier par un réel négatif change le sens de variation sur un intervalle,
et la fonction inverse aussi.
pour les tableaux, difficile de les confirmer sans le graphique de départ
(tu peux joindre un scan ou une photo du graphique, mais du graphique seulement : bouton Img sous la fenêtre de saisie).
pour la valeur interdite de k(x), regarde sur la courbe de f(x) à quel moment f(x)=0
Bonjour carita , merci de m'aider et de m'avoir expliquer pour le graphique.
f(x)=o en x=1 est donc la valeur interdite?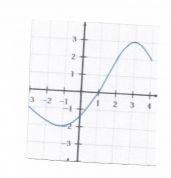
***image recadrée***
donc le tableau de variation de k est:
en sachant que 1 est la valeur interdite , je ne sais pas comment mettre les deux barre.
Est-ce correct
Bjr et merci Priam, je sais qu'il faut mettre une double barre mais je ne connais la méthode pour la mettre sur le forum
arawak oui, avec la double barre verticale sous le x=1,
c'est bon.
pas grave si tu ne sais pas la dessiner ici, le principal est qu'elle soit sur la copie.
sans cette valeur interdite, sur ton tableau de variation de 7h23 pour k(x)
on lisait cette incohérence : 
décroissance de -1/2 à 3 : pas possible.
à noter : pour déduire la variation de 1/u (u0) à partir de la variation de u,
il faut considérer des intervalles où la fonction est de signe constant.
bonne soirée à tous !
avec plaisir.
juste pour info, pour mettre les doubles barres sous la valeur interdite, perso je mets des |
(touche alt gr 6 sur clavier azerty)
sans les balises latex, tu verras mieux :
\begin{array} {|c|cccccccccc|} x & -3 & & -1 & & 1& & 3& & 4& \\ \\ {k(x)} & & \nearrow & & \searrow & || & \searrow & & \nearrow & & \end{array}
bonne suite !
Annuler
connectez vous