Inscription / Connexion Nouveau Sujet
Fonctions - Calculette TI 82
Bonjour,
Je comprends pas, j'aimerai vérifier ma dérivée et j'ai vu sur le net qu'il fallait aller dans MATH -> 8:nbreDérive( rentrer la dérivée.
Sauf qu'à chaque fois que je rentre ma dérivée, j'obtiens ERR:ARGUMENT
Cela signifie quoi?
Pour info ma fonction est:
B(x)= -x^2 + 208x - 64
Et en utilisant la formule : ax^2+bx+c = 2ax+b
J'ai B'(x)=2*-x+208
B'(x)=-2x+208
J'oublie de taper quelque chose dans ma calculette?
Bonjour
une TI 82 ne va pas te calculer une dérivée
mais seulement un nombre dérivé en "x0"
tu devrais regarder ta notice
elle doit avoir besoin qu'on lui donne x0 ou qq chose comme ça
et voici un lien qui répondra peut-être à ta question vis à vis de la TI
derrière nderive (fct, variable, nombre)
il lui faut 3 choses.....
Est-ce que mon étude de dérivée est bonne?
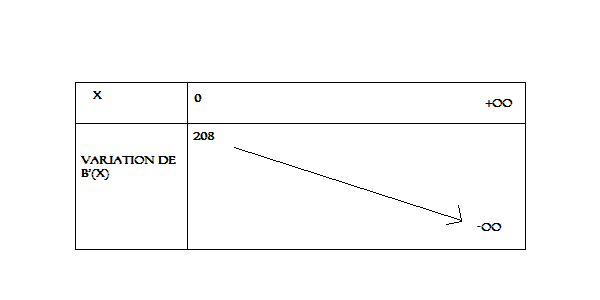
lim B'(x)=-2x+208=-oo
x->+oo
lim B'(x)=+oo
x->-oo
lim B'(x)=208
x->0
Pourquoi tu cherches des limites sur ta dérivée ? on cherche le signe de la dérivée (est ce qu'elle s'annule et pour quelle valeur ? puis son signe)
et les limites pour la fonction
sauf si ton énoncé te dit autre chose
Bah enfaite mon énonce me dis d'étudier la fonction B sur ]0;+oo[ et de donner son tableau de variation...
On m'a dit qu'il fallait voir la dérivée pour étudier la fonction B.
non, pas vraiment
ta dérivée vaut B'(x)= -2x+208
1re question à se poser
est ce que B'(x) peut être égal à 0
oui, pour -2x+208 = 0 soit 208 = 2x soit 104 = x
donc cette dérivée s'annule pour x=104
2e question à se poser
et quel est alors le signe de B'(x)
B'(x) est un polynôme du 1er degré qui s'annule pour x=104, et qui sera du coefficient existant devant "x" à droite de la solution
donc
x 104
B'(x) + 0 -
puis quand ta dérivée est positive, ta fct B est croissante
et quand ta dérivée est négative, ta fct B est décroissante
OK ?
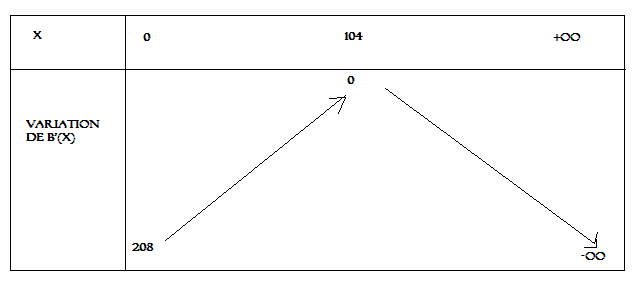
non,
B'(x) tu recopies le signe et la ligne en dessous, ce sont les variations de b avec les flèches
les lim en - l'infini ou + l'infini seront toutes les deux - l'infini
et tu devras calculer B(104) pour mettre en haut des flèches (le maxi)
désolée, je dois partir de manière urgente maintenant...
je me reconnecte ce soir.....
Ok merci en tout cas...
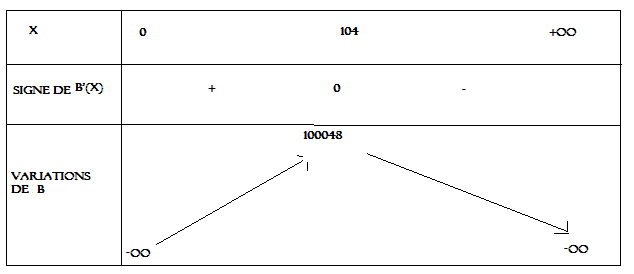
Donc ça me donnerai ça:
avec x=104 la valeur permettant de faire le bénéfice maximum correspondant à 10048 euros.
revenue devant mon ordi
tu as compris, OK
2 remarques
tout au début de l'exercice tu as écrit
ax^2+bx+c = 2ax+b
j'ai compris ce que tu veux dire mais tu ne peux pas l'écrire ainsi
mais comme ça : (ax^2+bx+c)' = 2ax+b
pour dire la dérivée de ...est....
moi je trouve 10752 comme maxi et non 10048
revois un peu
sinon, c'est bien !
Annuler
connectez vous