Inscription / Connexion Nouveau Sujet
Fonctions de référence
Bonjour, j'ai un Dm de maths pour lundi et je n'arrive pas bien , et ne comprend pas vraiment, comment faire un exercice , pouvez-vous m'aider s'il vous plait ? 
:s.
voilà l'énoncé :
Dans un repère othonormé (O,I,J) , on considère le cercle C de centre O et de rayon 1
Questions préliminaires :
1) justifier que le cercle C est l'ensemble des points M(x;y) tels que x²+y²=1
2)on s'intéresse maintenant au demi-cercle C' , formé par des points M de C d'ordonné positive ou nulle.
La courbe C' est la représentation graphique d'une fonction f.
Indiquer l'expression de f(x) et préciser son ensemble de définition.
Dans la suite de l'exercice , on suppose que pour tout réel x de l'intervalle [-1;1] , f(x)=
1-x².
On désigne par Cf sa courbe représentative dans un repère orthonormé (O,I,J)
On considère les points A(-1,0) et B(1;0).
Le point M est un point quelconque de Cf.
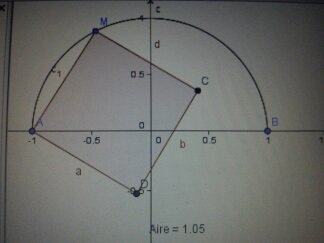
A partir des points A et M , on construit le carré AMCD comme indiqué sur la figure ci-dessous.
3) a l'aide d'un logiciel de géométrique dynamique (géogebre) ,réaliser la figure ci-dessus .
4) faire bouger le point M et compléter le tableau suivant après l'avoir recopié
| abscisse de M | -1 | -0.5 | 0.2 | 0 | 0.2 | 0.5 | 1 |
| Aire du carré AMCD |
5) conjecturer l'expression de l'aire du carré AMCD en fonction de l'abscisse de x de M.
6) exprimer l'ordonné de y de M en fonction de x
7) exprimer la longueur de AM en fonction de x
8)En déduire que l'aire du carré AMCD est un fonction affine de x
9)Calculer x pour que l'aire du carré AMCD soit égale à l'aire du demi-disque de diamètre [AB]
1) Puisque C est un cercle de centre O et possèdant un rayon de 1 , alors tous les points se situant sur ce cercle sont a une longueur de 1 par rapport au centre.
x²+y²=1 puisque c'est comme si 'lon utilisait le théorème de pythagore , l'abscisse au carré + l'ordonné au carré donne le plus grand coté du triangle , soit l'hypothénuse , soit le rayon
2) f(x)=V1-x² car avec le théorème de pythagore cela donnerai : 1=y²+x² donc y²=
1-x² ,l intervalle est [-1;1] puisque C' est formé des points M où le rayon est de 1.?
3) la figure est en bas du post
4)
| abscisse de M | -1 | -0.5 | 0.2 | 0 | 0.2 | 0.5 | 1 |
| Aire du carré AMCD | 0 | 1 | 1.6 | 2 | 2.4 | 3 | 4 |
5) lorsque l'abscisse de M est à -1 on voit que l'aire est 0 , à 1 l'aire est de 4 , sa a été " multiplier" par 4 ( je ne sais pas comment dire que sa à augmenter de 4 puis 0x4=0 mais bon....) , -0.5 à 0.5 sa a été multipilier par 3 ; -0.2 et 0.2 l'aire à été multiplier pas 2.
6)y=
1-x²
7)AM=
(-1-x)²x(1-x²)
( je pense que c'est faux :/
8)puisque et alors je déduis que l'aire du carré AMCD est un fonction affine de x
9)l'aire du demi disque de diamètre [AB]
l'aire d'un cercle est Pixrx2 , donc l'aire du demi-cercle est pixr , donc l'aire du demi disque est PI
apres pour trouver quand l'aire de AMCD soit égale à PI je ne vois pas trop comment il faut faire.
merci d'avance pour votre aide
Bonjour,
1)
Bon.
2)
Bon avec une faute de frappe :
y²=1-x²
donc y=(1-x²) -->tu as écrit y²=(1-x²)
ce qui donne :
f(x)=(1-x²)
4) Tu es censé remplir ton tableau avec ton logiciel Geogébra.
Il faut que la partie sous la racine soit 
0
soit :
1-x² 0
soit x² 
1
donc x 
[-1;1]
et Df=[-1;1]
J'envoie et je vois la suite.
6)
y²=1-x² car M est sur le demi-cercle.
y=(1-x²) --->déjà dit !
7)
AM²=(xM-xA)²+(yM-yA)=(x-(-1))²+(y-0)²=(x+1)²+y²
Mais y²=1-x² car M est sur le demi-cercle.
AM²=x²+2x+1+1-x²
AM²=2x+2
Il faut 2x+2 0
soit x -1 qui est bien vérifié.
AM=(2x+2)
8)
Mais AM² est l'aire du carré AMCD donc :
aire du carré AMCD =2x+2 qui est bien une fct affine.
On peut vérifier que ton tableau est bon à la 4) (sauf un -2 où tu as marqué 2 sur la; ligne "x") !!
9)
aire demi-cercle=
*1²/2=/2
Il faut résoudre :
2x+2=/2
2x=/2 - 2
x=(/4) - 1
...sauf inattentions...
Merci de m'avoir répondu
mais est-ce que la 5) est juste ? personnellement je la trouve mal formuler :/
et pour la 7) pourquoi :
AM²=(xM-xA)²+(yM-yA)²?
c'est comme pour calculer les coordonnées d'un vecteur on dirait, enfin sans les ².
merci de m'éclairer
mais est-ce que la 5) est juste ? personnellement je la trouve mal formuler :/
En effet , ta réponse que je n'avais pas lue (!!) n'est pas bonne.
Tu dis :
On remarque que le rapport :
augmentation de l'aire/augmentation de l'abscisse est constant.
(1-0)/(-0.5-(-1))=2
(1.6-1)/(-0.2-(-0.5)=2
(2-1.6)/(0-(-0.2)=2
Etc.( Tu peux tout faire si tu veux)
Donc : aire AMCD=2x + b
Il faut "b". Par ex. , on a :
pour x=0 ,aire =2
donc : 2=2*0+b qui donne b=2
aire AMCD=2x + b
et pour la 7) pourquoi :
AM²=(xM-xA)²+(yM-yA)²?
C'est vu en classe de 3ème . C'est une application de Pythagore .
Va voir le paragraphe 3) de cette page :
Bonjour, j'ai le même exercice à faire et je ne comprend pa poourquoi dans la 9) x=(/4) -1
Esceque vous pouriez m'expliquer ?
Il faut résoudre :
2x+2=/2
2x=/2 - 2
(1/2)(2x)=(1/2)(/2 - 2)--->tu comprends ça ? Ce qui donne :
x=(1/2)(/2) - (1/2)(2)
x=/4 -1
Tu as 2x à gauche et tu veux "x" tout seul. OK ?
Dans mon 1er envoi du 26 à 11 h 36, j'ai divisé les membres de gauche et de droite par 2 et tu n'as aps compris.
Alors là, je me suis dit : je vais multiplier les membres de gauche et de droite par 1/2 , ce qui est la même chose que de diviser par 2 et tu ne comprends tjrs pas.
Je fais un dernier essai .
Si tu as :
2x=y-3 (Rien à voir avec cet exo bien sûr)
alors :
x=y/2 - 3/2
Je ne peux rien faire de plus .Désolé.
Pardon, en fait je n'avais pas compris car je n'est pas l'habitude de le marquer de cette façon et quand je l'ai fait je n'ai pas réussi à trouver le bon résultat donc j'ai pensé que vous aviez utilisé une autre méthode. Je vous remercie de m'avoir aidé, cela m'a été très utile. Au revoir, merci.
Bonjour j'ai le même exercice, et ma seule partie que je n'ai pas compris c'est la question 2), d'où sort les calcul (1-0)/(-0,5-(-1)=2 ?
Pour Chaton78
J'ai dû tout relire pour trouver de quelle question tu parlais car ce n'est pas la 2) mais :
5) conjecturer l'expression de l'aire du carré AMCD en fonction de l'abscisse de x de M.
On observe dans le tableau de la question 4) envoyé par Murphy04 que le rapport :
accroissement de l'aire/accroissement de l'abscisse
est constant.
Pour le montrer , on fait donc qq. calculs .
Quand on passe de x =-1 à x=-0.5 :
accroissement de l'abscisse=(-0.5-(-1))=0.5 ; accroissement de l'aire correspondant=(1-0)=1
Rapport : accroissement de l'aire/accroissement de l'abscisse=1/0.5=2
Quand on passe de x =-0.5 à x=0.2:
accroissement de l'abscisse=(0.2-(-0.5))=0.3 ; accroissement de l'aire correspondant=(1.6-1)=0.6
Rapport : accroissement de l'aire/accroissement de l'abscisse=0.6/0.3=2
Etc.
Reporte-toi ensuite à ma réponse à la question 5)
Ah d'accord !.. Merci beaucoup !
Mais pour la question 7) exprimer la longueur Y de M en fonction de x. A un moment on trouve AM^2= x^2+1 , c'est pas l'identité remarquable a^2+b^2= a^2+2xab+b^2 qu'il faut développer ?
Désolé mais je n'ai vu nulle part dans la 7) :
A un moment on trouve AM^2= x^2+1
Par contre , en relisant ma réponse à la 7) , j'ai vu carré qui manquait . Je corrige donc ma réponse . Il faut lire :
7)
AM²=(xM-xA)²+(yM-yA)²=(x-(-1))²+(y-0)²=(x+1)²+y²
Mais y²=1-x² car M est sur le demi-cercle.
AM²=x²+2x+1+1-x²
AM²=2x+2
J'avais oublié le carré dans (yM-yA)² mais il est réapparu ensuite.
Ce n'est pas l'identité remarquable a^2+b^2= a^2+2xab+b^2 qu'il faut développer ?
L'identité dont tu parles est :
(a+b)²=a²+2ab+b²
Il faut savoir les identités remarquables apprises en 3ème par coeur !! Sinon tu cours à la catastrophe !!
Les voici :
(a+b)²=a²+2ab+b²
(a-b)²=a²-2ab+b²
a²-b²=(a+b)(a-b)
Ah d'accord c'est donc la dernière que vous avez développé pour AM, c'est ça?
Non c'est pas ça, je pense avoir compris, mais je comprends pas pourquoi vous dites que c'est une application de Pythagore....
Une application de Pythagore donnerai :
AM^2= Ax^2+Bx^2
Avec AM l'hypothenuse et Ax et Bx les deux autres côtés, non?
Je comprends pas trop....
Bonjour,
j'ai tapé ma réponse de 22 h 46 hier avec une tablette et j'ai dû laisser traîner mon doigt pour écrire un "bg" qui ne veut rien dire après ma phrase !!
Passons à ta demande :
Une application de Pythagore donnerait :
AM^2= Ax^2+Bx^2
Avec AM l'hypothenuse et Ax et Bx les deux autres côtés, non?
Ce que tu écris n'est pas clair du tout, du tout et sûrement faux.
Tu vas projeter le point M sur l'axe des "x" en un point qu'on va appeler P , par exemple.
Donc le triangle APM est rectangle en P. Tu me suis ?
Pythagore :
AM²=AP²+PM²--->ligne (1)---> ( tu as une touche pour le carré en haut et à gauche du clavier).
Mais P et M ont même abscisse qui est donc x d'après l'énoncé. OK ?
Donc AP²=(xP-xA)² mais comme xP=xM=x , alors : AP²=(x-xA)². Mais xA=-1 donc AP²=(x-(-1))²=(x+1)². Toujours OK ?
PM²=(yM-yP)²
Mais yM=y d'après l'énoncé et comme P est sur l'axe des x , alors yP=0 donc ;
PM²=(y-0)²=y²
Finalement la ligne (1) devient :
AM²=(x+1)²+y²-->ligne (2)
Ce n'est pas fini car dans la question 1) , on a montré que : x²+y²=1 donc que : y²=1-x².
Donc la ligne (2) devient :
AM²=(x+1)²+1-x²-->ligne (3)
On développe (x+1)² en utilisant l'identité remarquable: :
(a+b)²=a²+2ab+b²
que tu connais bien maintenant !!
Et la ligne (3) devient :
AM²=x²+2x+1+1-x²
AM²=2x+2
Comme un carré doit être
0 , il faut : 2x+2 0 soit x -1 qui est vérifié d'après l'énoncé .
Donc :
AM=
(2x+2)
Que puis-je faire de plus pour que tout soit clair pour toi ? ?
Je viens de lire sur ton profil que tu es en 1ère S. C'est ton prof de maths de 2nde qui t'a conseillé de faire S ? Tu as intérêt à travailler dur ...
La c'est claire merci beaucoup.
Et merci de votre charmante remarque
Je viens de lire sur ton profil que tu es en 1ère S. C'est ton prof de maths de seconde qui t'as conseillé de faire S? Tu as intérêt à travailler dur....
Oui je suis en 1ère S, et non personne me l'as conseillé, au contraire même. Je sais que j'ai des difficultés et même que je vaut pas un clou en maths. Mais je préfère poser des question et comprendre ce que je fais, plutôt que de faire du simple recopiage car c'est ce que j'aurais pu faire des le départ.
Ne vous inquiétez pas je travail dur, et je pense d'ailleurs que c'est pour ça qu'en 1ère S j'ai 16 de moyenne.
Annuler
connectez vous