Bonjour gigibon

Asymptote verticale => valeurs interdites pour x

Quelles seraient la/les valeurs interdites pour x ?

Philoux

Bonjour,

Pour trouver une asymptote verticale,il faut calculer les limites aux bornes de ta valeur interdite,ici 5

lim x->5^- F(x)=+

Et lim x->5⁺ F(x)=-

Donc x=5 est asymptote verticale a F(x)

Et surtout n'hésite pas pour d'autres questions!

Salut!

Désolé philoux!!

A chaque fois je file la réponse sans faire chercher!

Encore désolé!!

>gigibon

Au fait, gigibon, as-tu trouvé une/des asymptote(s) horizontale(s) ?

Philoux

>ludo 13:16

pas de soucis

Philoux

Ta dérivée :


Pour ton asymptote verticale, il te faut chercher un scalaire L tel que

Limite de F sous entendu ...

Bonjour à tous

Attention tout de même, la "propriété" qui dit qu'il y a asymptote verticale pour les valeurs interdites de x ne marche que pour les fonction rationnelles.


Jord

Salut davidk

pourquoi pas -oo ?
Philoux

Petit aparté sur le programme de Tle S à venir :

F induit une bijection de .

L'équation F(x)=0 admet une unique solution dont un encadrement à 10^-2 près vaut :

>NM

Attention tout de même, la "propriété" qui dit qu'il y a asymptote verticale pour les valeurs interdites de x ne marche que pour les fonction rationnelles.

Pas seulement :

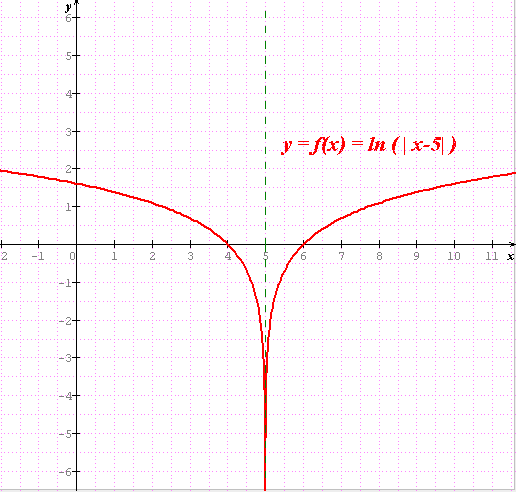
y = ln( |x-5| )

Philoux

>david

de R vers R ?

T'es sûr ?

Philoux

Euh davidk .... Pourquoi faire un encadrement d'une solution dont tu peux donner la valeur exacte ?



De plus F n'est définie que sur R-{5} donc ne peut pas induire une bijection sur R tout entier


Jord

Oui Philoux , mais ce que je voulais dire c'est que pour d'autre fonction sous forme de quotient comme ça ne marchait pas.


Jord

Nightmare : bijection déduite de mon tableau de variations.
Ma Ti-82 m'indique une fonction croissante de forme hyperbolique sur  moins infini ; 5 juxtaposé d'une asymptote verticale en 5 aiguisé d'une deuxième boucle hyperbolique en 5 + infini.

Donc ce qui confirme ce que j'ai dit.

De plus, si je ne m'abuse ne serait-ce pas une bijection de :

R-{5} -> R-{2} ?

( au fait, quand dit-on "vers", quand dit-on "sur" ? )

Philoux

Re

davidk , dans ce cas là quel est le/les antécédents de -2 par F ?

Philoux , je pense que c'est sur R-{-2} et non sur R-{2}.

Personnelement je dit sur , je ne sais pas si l'on peut dire vers
Le plus simple est de dire que :

est une bijection



Jord

bien vu sur le -2

y'a pas un distingo selon la nature :

- injectivité
- surjectivité

?

Philoux

R-{-2} NM



Philoux

Oups la boulette

Non non, j'ai toujours lu "sur" où parfois "dans" mais jamais "vers" quelque soit la jectivité


Jord

bonjour,


par le procede de la division des polynomes ou celui des equivalence de coefficient de x de meme degre que l'on apprend en 1° on trouve facilement que


ce qui nous demontre la presence d'une asymptote verticale quand x tend vers + ou - l'infini

voila ce que j'en pense

a plus tard
Paulo

Bonjour paulo

Cette méthode s'avére utile lorsque la partie entiére de la fraction est une fonction affine.

Ici il suffisait de factoriser par 2x en haut et -x en bas et c'était reglé.


Jord

>non paulo

le -2 est représentatif d'une asymptote horizontale

voila ce que j'en pense

a plus tard
Philoux

Par ailleurs

asymptote verticale quand x tend vers + ou - l'infini

sont contradictoires

Philoux

re
excusez_moi j'etais en train de retourner sur le site pour dire que c'etait un asymptote horizontale. je m'etais rendu compte de mon erreur . merci de votre reaction
Paulo

pas de soucis paulo

Philoux

merci a tous
j'avais deja etudie la fonction a fond avec sens de variation etude du signe de F' et tout j'avais meme trouve l'asymptotehorizontale mais grace a vous je trouve maintenant la verticale en x=5
merci encore
par ocntre ac vos ln j'ai failli m'embrouille
enfin merci a tous ciao
gigibon

Ce fut un plaisir


Jord