Inscription / Connexion Nouveau Sujet
Fonctions polynômes et lecture graphique
Bonjour  J'ai quelques soucis avec exercice donc voilà l'énoncé :
J'ai quelques soucis avec exercice donc voilà l'énoncé :
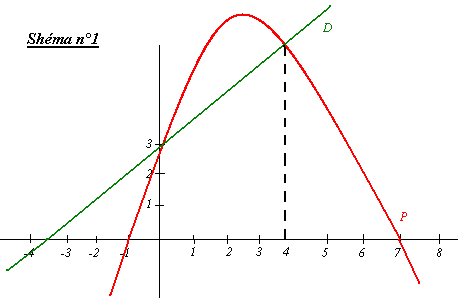
Dans un repère orthonormé, D est la droite et P est la parabole représentées ci-dessous (voir shéma n°1).
D représente une fonction affine x --> mx + p
P représente une fonction polynôme de second degré x --> ax²+ bx +c
f est la fonction x --> mx + p
¯¯¯¯¯¯¯¯¯¯¯¯
ax²+ bx +c
1) A l'aide du graphique, déterminer en justifiant :
a. L'ensemble de définition de f
b. l'ensemble des solutions de l'équation f(x)= 0
c. l'ensemble des solutions de l'équation f(x)= 1
d. le signe de f(x)
2. C est la courbe représentant f dans un repère orthonormé. Interpréter
graphiquement chacun des résultats obtenus à la question 1).
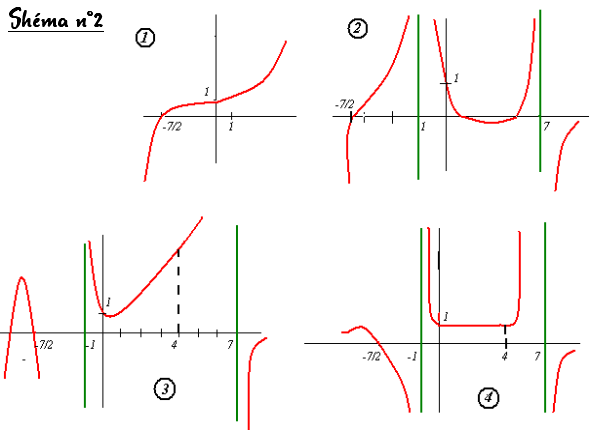
3) Parmi les courbes suivantes (voir shéma n°2), laquelle est la seule
suceptible de représenter f ? Justifier la réponse.
Merci d'avance pour votre aide 
Pour la question
1)a. je pense que l'ensemble de définition de f est R étant donné que la fontion affine mx + p et l'expression de second degré ax²+ bx +c sont définies dans R. (je ne sais pas si la justification est juste)
b. Pour trouver les solutions de f(x)=0 on regarde les points d'intersection entre f et l'axe des abscisses. Les solutions sont -7/2 ; -1 et 7.
c. Pour f(x)=1 je sais qu'il y a 3 solutions mais je ne sais pas comment les définir...
Je ne sais pas si tout ça est correct et pour le reste je ne sais pas comment m'y prendre...
Pour la question
1)a. je pense que l'ensemble de définition de f est R étant donné que la fontion affine mx + p et l'expression de second degré ax²+ bx +c sont définies dans R. (je ne sais pas si la justification est juste)
Attention, en imaginant que ax² + bx + c = 0 ta fonction f n'est pas définie. Je ne dis pas que c'est le cas, mais il faut y penser.
b. Pour trouver les solutions de f(x)=0 on regarde les points d'intersection entre f et l'axe des abscisses. Les solutions sont -7/2 ; -1 et 7.
f c'est la courbe rouge
c. Pour f(x)=1 je sais qu'il y a 3 solutions mais je ne sais pas comment les définir...
Non.
1)a. Donc on peut dire que la fonction f existe si l'expression ax²+bx+c au dénominateur ne vaut pas 0. Donc il faut résoudre l'équation
ax²+bx+c =/= 0
a(x-x')(x-x")=/= 0
Donc D= R-{x'; x"}
D= R-{-1 ; 7}
b. Les solutions de f(x)= 0 sont -1 et 7
c. Pour cette question je ne sais pas on ne voit pas les graduations des points concernés sur le graphique...
Je résume :
Dans un repère orthonormé, D est la droite et P est la parabole
D représente une fonction affine x --> mx + p (c'est la droite verte)
P représente une fonction polynôme de second degré x --> ax²+ bx +c (c'est la courbe rouge du schéma 1)
f est la fonction x --> (mx + p)/(ax²+ bx +c) (c'est l'une des courbes rouges du schéma 2)
D'accord, pour que f soit définie, il ne faut pas que ax² + bx + c = 0
donc -1 et 7 sont exclus on est d'accord.
Je t'ai dit une bêtise tout à l'heure, la 1e courbe rouge est la parabole, pas f
On cherche x tel que f(x) = 0 autrement dit (mx + p)/(ax²+ bx +c) = 0
Tu vois quelles valeurs de x annulent f(x) ?
Je dirais que d'après le graphique, les valeurs qui annulent f(x) sont -7/2 ; -1 et 7 étant donné que ce sont les points d'intersection entre la fonction et l'axe des abscisses... Mais je ne suis pas sure.
En lisant le graphique, l'équation de la droite D est y= 6x/7 +3. Donc :
mx +p = 0
6x/7 +3 = 0
6x/7 = -3
6x = -21
x = -21/6 = -7/2
C'est donc bien l'intersection entre la droite et l'axe des abscisses 
Mais après pour f(x)= 1...
Je fais (mx +p)/(ax²+bx+c)-1 = 0 en remplaçant mx+p par 6x/7+3 ?
f(x) = 1
(mx + p)/(ax²+ bx +c) = 1
donc (mx + p) = (ax²+ bx +c)
quels sont les points qui vérifient cette égalité ?
Eh bien en regardant le graphique les solutions de l'équation sont 0 et 4 (les abscisses des points d'intersection entre la courbe et la droite). Mais en la résolvant je ne trouve pas du tout ces solutions...
J'ai d'abord cherché l'expression de la courbe, sachant qu'elle a 2 racines solution x'= -1 et x"= 7 :
ax²+bc+c = a(x- x')(x- x") = (x+1)(x-7) = x²- 7x +x -7 = x²-6x-7
Et sachant que l'équation de la droite D est y= 6x/7 +3, je résoud f(x)= 0 :
(6x/7 +3)/(x²-6x-7)= 1
(6x/7 +3)/(x²-6x-7)= (x²-6x-7)/(x²-6x-7)
(6x/7 +3) = (x²-6x-7)
(6x+21)/7 = (7x²-42x-49)/7
(6x+21) = (7x²-42x-49)
6x+21-7x²+42x+49 = 0
-7x²+48x+70 = 0
Ensuite j'ai cherché le discriminant du polynôme -7x²+48x+70 :
delta = b²- 4ac = 48²- 4(-7)x 70 = 4264 > 0 dc il y a 2 solutions
s'= (-b- V4264)/ 2a = (-48- V4264)/-14
s"= (-b+ V4264)/ 2a = (-48+ V4264)/-14
Donc les solutions de f(x)= 1 sont normalement (-48+ V4264)/14 et (48- V4264)/14. Mais ça ne correspond pas à ce qu'on voit sur le graphique...
Les solutions sont 0 et 4, ce sont les points d'intersection de la droite et de la parabole, vus sur le graphique.
Aucune démo n'est demandée.
Si, On demande de justifier dans l'énoncé... Je pense avoir trouvé la méthode mais il y a un problème dans les calculs...
A l'aide du graphique = lecture graphique, on ne demande pas de trouver a b et c
Si ça t'intéresse, je les ai calculés, mais c'est hors sujet.
Ahh d'accord dans ce cas si c'est hors-sujet je laisse tomber. En fait je voulais juste savoir comment on faisait par le calcul ^^.
Mais comment-avez-vous fait pour trouver -3x²/7 + 18x/7 + 3 ? Parce que j'ai calculé en utilisant les racines de l'équation de la courbe je n'ai pas trouvé ça...
ok je laisse les calculs de côté.
Maintenant il faut déterminer le signe de f(x)... J'ai fait la question mais je ne sais pas si c'esr bon :
- f < 0 sur ]- ; -7/2[
; -7/2[
- f(x)> 0 pour x  [-1 ; 7]
[-1 ; 7]
- f(x)< 0 x  ]-
]- ; -1[
; -1[ ]7; +
]7; + [
[
C'est ça ?
Tu ne peux pas mettre l'équation de la parabole, car tu n'est pas censé la connaître.
Mais les réponses sont bonnes.
D'accord 
Je peux me débrouiller pour la suite. En tout cas merci beaucoup pour votre aide et d'avoir été là jusqu'au bout ^^. Bisous et bonne continuation !