Inscription / Connexion Nouveau Sujet
forme canonique d'une fonction absolue
Je voudrais juste des précision par rapport à une variable dans la forme canonique de la fonction valeur absolue : f(x) = A | B(x - H) | + K
Le B il sert à quoi? quels sont les impacts sur un graphique de la fonction?
Merci d'avance.
peut-être je m'exprime mal... mais j'ai trouvé la réponse à ma question.
La forme canonique de la fonction valeur absolue est f(x) = A | (x - H) | + K où le sommet est déterminé par (h,k) et A donne la pente de la fonction.
J'ai une autre question : Comment on trouve l'équation d'une fonction sinus?
OK pour la "forme canonique" de la fonction valeur absolue : elle permet de se ramener, avec un changement de l'origine du repère, à la fonction f définie par f(x)=a|x|.
Par contre, je ne dois pas être bien réveillé ce matin : je ne comprend pas non plus ta question concernant la fonction sinus... S'il s'agit de se ramener à une fonction "basique", peut-être f(x)=a sin(x-h)+k ?
C'est ce que je cherchais : f(x)=a sin(x-h)+k, j'avais fait une recherche sur internet et je ne l'avais pas trouvé. Merci beacoup!
Comment fais-je pour avoir une fonction de valeur absolue sous la forme canonique???
Voici la fonction: f(x) = |7x-1|-4
je ne savais pas que ça existait mais regarde ici : 
c'est expliqué.
Pour f(x)=|7x-1|-4, si on veut la mettre sous la forme f(x) = A | B(x - H) | + K alors visiblement, il faut faire :
f(x)=|7x-1|-4 =|7(x-1/7)|-4 =7|x-1/7|-4 et A=7 ; B=1; H=1/7 ; K=-4
Bonjour j'aurais une question sur la forme canonique de la |VA|c'est au programme en Suisse.
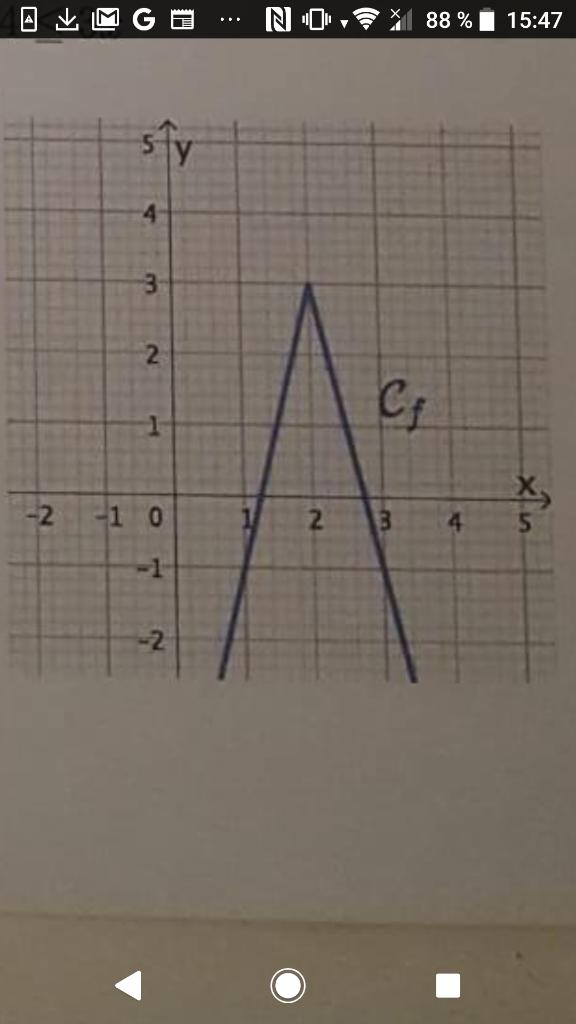
Si j'ai bien compris vos messages ma fonction ici serait a|x-2|+3
Car le sommet a pour coordonnées (2;3) mais la pente est différente pour chacune des demi droites donc a=4 ou a=-4?
Merci
Bonjour
la fonction "valeur absolue" donne un V
si tu multiplies par un nombre positif, tu conserves l'allure en "V", en écartant ou resserrant l'angle de la pointe
si tu multiplies par un nombre négatif, en plus tu retournes ton "V"
Ici tu as un "V" renversé : c'est donc un coeff négatif qu'il te faut
Annuler
connectez vous