Inscription / Connexion Nouveau Sujet
Fourmi sur un cube
Bonjour ! je suis bloque sur ce probleme ! si quequ'un peut m'aider ! merci !
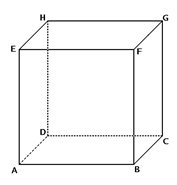
Une fourmi se deplace de maniere aleatoire sur les aretes du cube ABCDEFGH en allant toujours d'un sommet a un autre en parcourant une arete et en choisissant au hasard une des trois directions possibles a chaque sommet.
Le but de l'exercice est de calculer la probabilite d'aller a un sommet au sommet oppose en 3 deplacements. ( que veulent-ils dirent par oppose ??)
1) Decrire a l'aide d'un arbre les chemins a deux etapes partant de A; combien sont-ils ?
2) Quelle est la probabilite de revenir en A apres deux etapes ?
3) Parmi tous les chemins possibles, combien aboutissent a un sommet voisin de G ?
je suppose que les sommets voisins sont H,F et C , n'est ce pas?
4) En deduire la probabilite d'atteindre G a la troisieme etape ?
1/4 ? vu qu'il y quatre sommets ( H,F,C et G )
Merci pour votre future aide 
Bonjour,
Deux sommets sont dits opposés si la droite qui passe par ces sommets passe également par le centre du cube :
E et C, H et B, G et A, F et D.
Pour la 1) :
Partant de A, tu peux aller en B, D, E
Ensuite :
Partant de B, tu peux aller en A, C, F
Partant de D, tu peux aller en A, C, H
Partant de E, tu peux aller en A, F, H
Donc partant de A, les chemins à 2 étapes sont :
A, B, A
A, B, C
A, B, F
.......
A, E, A
A, E, F
A, E, H
Je te laisse les écrire tous, au total il y en a 3*3 = 9
Pour le 2), les chemins à 2 étapes qui reviennent en A sont évidemment :
A, B, A
A, D, A
A, E, A
Il y en a 3, donc la probabilité est 3/9 = 1/3
Essaye de continuer tout seul...
Bonjour, je ne comprend pas la derniere question de cet exercice!
Je pense que la reponse c'est 2/9 mais je en sais pas comment l'expliquer!
Merci pour votre aide !
Pour le 1, j`ai fait l`arbre et il y a 9 chemins differents.
Pour le 2, j`ai dit qu`il y avait 3 chemins qui termine par A, donc 3/9=1/3.
Pour le trois, j`ai dis que les sommets voisins de G sont H,F et C. En regardant sur mon arbre j`ai vu 2 chemins terminait par H, 2 par F et 2 par C donc il y a 6 chemins qui terminent sur un sommet voisins de G
Pour le 4, je n`arrive pas a expliquer.
Je me suis dit que vu qu`en 2 etapes la fourmi fait 9 chemins et que chaque sommet du cube a trois sommets voisins on a 9*3 chemins differents de 3 etapes.
Apres j`ai fait 6/27 se qui donne 2/9.
Peu tu me dire si c`est juste ou pas ....
merci beaucoup !
Ton résultat est juste, ta justification est un peu faible.
Je dirais plutôt que la probabilité d'atteindre un sommet voisin de G à la deuxième étape est P1 = 2/3
Justification : 9 cas possibles d'après 1), 6 cas favorables d'après 3), donc P1 = 6/9 = 2/3
Ensuite, partant d'un sommet voisin de G, la probabilité d'atteindre G est P2 = 1/3
Le troisième saut étant un évènement indépendant des deux premiers, la probabilité globale (atteindre G en 3 coups) est le produit des probabilités de chaque étape (2 coups pour arriver en position favorable au troisième coup et le troisième coup pour arriver en G)
Donc P = P1.P2 = (2/3).(1/3) = 2/9