Inscription / Connexion Nouveau Sujet
Graphique d'une suite
Bonjour, j'ai un exo à faire sur les suites mais je sais pas trop comment lire ce genre de graphique c'est la première fois que j'en vois un
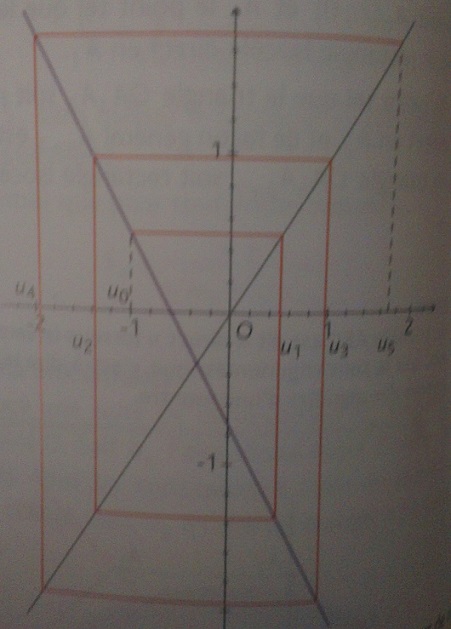
On a représenté graphiquement les premiers termes de la suite (Un).
D'après le graphique que peut-on dire sur les valeurs de Un lorsque n tend vers +infini ?
A première vue la suite semble être géométrique et comment on lit n tend vers +infini?
Bonsoir,
"ce genre de graphique" est classique pour représenter graphiquement une suite
Un considère une suite définie par une relation de récurrence Un+1 = f(Un) où f est une fonction quelconque
ici f(x) est une simple droite (à peu de choses près y = -(4/3)x - 4/5 )
c'est à dire la suite définie par Un+1 = -(4/3)Un - 4/5
avec U0 = -1
alors U1 représente l'ordonnée du point d'abscisse U0 sur la courbe f(x) : on "renvoie" verticalement U0 sur la courbe
on reporte cette valeur U1 (verticale) sur l'axe des abscisses (horizontal) en renvoyant ce point par une horizontale sur la droite y = x.
l'abscisse de ce nouveau point est donc U1 et renvoyé verticalement sur l'axe des x.
Et on recommence autant qu'on veut pour obtenir U2, U3 ...
en renvoyant alternativement par une verticale vers f(x) et par une horizontale vers y = x
la suite est matérialisé par les abscisses des points successifs.
un exemple avec une autre fonction f(x), du second degré :
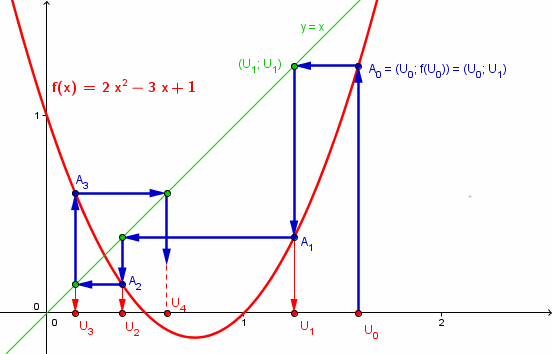
les abscisses des points A0, A1, A2 ... sont les valeurs de la suite U0, U1, U2 ...
ta suite est beaucoup plus simple que celle là puisque la fonction f(x) est une simple droite
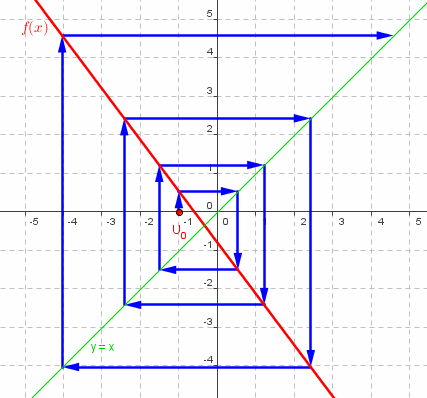
"faire tendre n vers l'infini" c'est augmenter indéfiniment le nombre de "boucles" d'itérations
Il est visible que cette suite croit indéfiniment en valeur absolue (alternativement >0 et <0)
reste à savoir si elle atteint une limite ou bien si elle croit vers l'infini en valeurs absolues.
pour cela tu as presque répondu : "la suite semble géométrique"
en fait elle ne l'est pas : le rapport de deux valeurs successives n'est pas constant
Mais si on "décale" l'origine au point d'intersection de f(x) et de y = x, cela devient une suite géométrique par rapport à cette nouvelle origine (un coup du père Thalès) et donc croit vers l'infini (en valeur absolue).
Merci pour l'aide donc pour justifier je peux dire que si n est pair ou impair alors les valeurs de Un sont négatives ou positives, donc si la suite n'est pas géometrique , elle est quelconque ?
la raison d'une suite géométrique peut être négative et alors la suite est alternativement positive et négative, ça ne l'empèche pas d'être géométrique !
par exemple la suite
1, -2, +4, -8, +16, .... Un = (-2)n est bien une suite géométrique de raison -2
ici le problème est que même en valeur absolue (si tu changes de signe tous les termes négatifs) la raison n'est pas constante.
sur le graphe on "lit" environ (graphe pas très précis)
U0 = -1
U1 = 0.5 U1/U2 = -0.5
U2 = -1.4 U2/U1 = -2.8
U3 = 1 U3/U2 = -0.7
U4 = -2 U4/U3 = -2
U5 = 1.7 U5/U4 = -0.75
le rapport Un+1/Un est loin d'être constant !
la précision du graphe est insuffisante pour en dire plus
il faudrait calculer les valeurs précises pour voir qu'en ajoutant à cette suite une certaine valeur constante (de l'ordre de 0.4) la nouvelle suite Vn obtenue est une suite géométrique
la suite Un est ce qu'on appelle une suite "arithmético-géométrique" donc pas tout à fait quelconque 
suite géométrique : Un+1 = r Un
Un
suite arithmétique : Un+1 = r + Un
suite "arithmético-géométrique Un+1 = a Un + b
Un + b
suite "quelconque" n'importe quoi d'autre
ici on a Un+1 = a Un + b où y = ax + b est l'équation de la droite descendante
Un + b où y = ax + b est l'équation de la droite descendante
merci beaucoup pour les explications, j'ai enfin compris pourquoi c'était une suite arithmético-géométrique et comme ta dis, la raison n'est pas constante elle varie à chaque fois, donc je justifie pour "D'après le graphique que peut-on dire sur les valeurs de Un lorsque n tend vers +infini ?"
que c'est une suite arithmético-géométrique, que la raison n'est pas constante et je justifie en donnant les 5 premiers termes + les vérifications en divisant par le terme précédent, donc si les valeurs de Un est pair ou impair alors les valeurs de Un sont négatives ou positives
Oui mais on te demande "lorsque n tend vers +infini ?"
il faut donc que tu justigfie que en valeur absolue les termes tendent vers l'infini et pas ver une limite finie du geure 5000.
et ceci se justifie en "décalant" la suite en recentran,t l'origine des coordonées au pont d'intersection
alors la suite déc


