Inscription / Connexion Nouveau Sujet
Hyperbole équilatère
Bonjour, je cherche de l'aide pour cet exercice. J'en suis à la 2eme question.
Sur l'hyperbole équilatère d'équation xy=k, on considère les points fixes A et A' d'abscisses a et -a ainsi qu'un point variable M d'abscisse m.
1) Calculer les coefficients directeurs des droites MA et MA'. Montrer qu'ils sont opposés. Comparer les directions des bissectrices de l'angle AMA' à celles des asymptotes Ox et Oy. En déduire q'une hyperbole équilatère est définie par son centre O et deux de ses points. Donner la construction de ses asymptotes.
2) Soit B un point fixe de l'hyperbole distinct de A, A' et M. Démontrer que les angles BAM et BA'M sont égaux ou supplémentaires suivant que la droite BM coupe ou non le segment AA', puis que les cercles BAM et BA'M sont égaux et symétriques par rapport à la droite BM.
3)Etant donnés trois points A,B,C, en déduire que le lieu du deuxième point d'intersection de deux cercles égaux variables, le premier passant par A et B, le second par B et C, est l'hyperbole équilatère passant par A, B et C admettant pour centre le milieu O de AC.
Je n'arrive pas à démontrer que les angles BAM et BA'M sont supplémentaires.
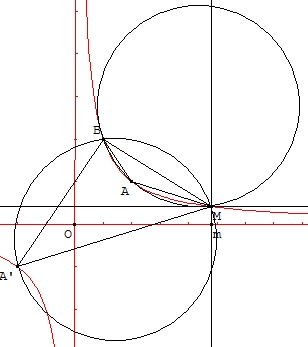
Si deux angles inscrits interceptent le même arc AB, ils sont égaux si leurs sommets sont située du même côté de la corde AB, ou supplémentaires si leurs sommets sont situés de part et d'autre de cette corde.
Mais il faut bien considérer un seul cercle pour pouvoir parler de sommets du même côté ou non de la corde commune.
Bonjour,
Pour démontrer la question 2, tracer les bissectrices des angles BAM et BA'M pour voir les angles respectivement égaux...
Bonjour,
la question est prise à l'envers !!
démontrer que les angles sont égaux ou supplémentaires
PUIS (en déduire) que les cercles etc ...
l'idée est peut être de partir des bissectrices de AMA' et de ABA' qui sont parallèles ou perpendiculaires (puisque toutes deux parallèles aux asymptotes, question 1)
pas le temps de réfléchir d'avantage dans l'immédiat
je voulais dire
les cotés des angles BAM et BA'M, BA et BA' d'une part, MA et MA' d'autre part ayant des directions symétriques par rapport aux directions des asymptotes (ou des bissectricesen B et M), les angles BAM et BA'M sont bien éguaux ou supplémentaires.
Bonjour,
Si on sait manipuler les angles de droites (définis à près), ça se passe bien en utilisant 1)