Inscription / Connexion Nouveau Sujet
Intersections de courbes
Bonsoir, je viens d'effectuer un exercice pourriez vous me corriger et m'aider s'il vous plait.
Enoncé:
On considère, dans le plan muni d'un repère:
l'hyperbole d'equation y= 2/x et la droite d'equation y= 1/2x-3/2
a. A l'aide de la calculatrice, conjecturer les coordonées des points d'intersection de ces deux courbes. ( je vous avoue que j'ai eu un peu de mal pour cette question mais j'ai qaund même essayé )
b. Montrer que déterminer l'abscisse des points d'intersection de ces deux courbes revient à résoudre ,dans R* l'equation x^2-3x-4=0.
c. Résoudre cette équation, puis confirmer ou infirmer la conjecture de la question a.
delta= -3^2-4*1*(-4)
delta= 7
x1=-(-3)-racine de 7/2*1= 3-racine de 7 sur 2
x2= 3+racine de 7 sur 2
Bonjour,
a) A l'aide de la calculatrice, conjecturer
cela veut dire lire graphiquement des valeurs approchées de ces coordonnées
b) 2/x = 1/2 x -3/2 etc
c) calcul faux
delta= -3^2-4*1*(-4)
ne pas confondre -(3²) et (-3)² !!
puis comparer les valeurs approchées conjecturées question (a) avec le résultat du calcul (une fois corrigé)
A l'aide de la calculatrice, conjecturer les coordonées des points d'intersection de ces deux courbes. ( je vous avoue que j'ai eu un peu de mal pour cette question mais j'ai qaund même essayé )
On te demande tout simplement de lire sur ton graphique les abscisses des points d'intersection de ces 2 courbes...
c) Ton delta est faux !!
c'est (-3)² et non pas -3² ... b = -3 !! Grosse différence...
Ahhh ouii... C'est l'ensemble qui est au carré ducoup ça me donne delta=25
Donc
x1=-(-3)-racine de 25/2*1
x1= -1
x2=-(-3)+racine carré de 25/2*1
x2=4
Les solutions sont donc -1 et 4?
C'est mieux ...
Et tu compares ceci avec la conjecture que tu as faite à la question a) !
A présent il ne te reste plus qu'à traiter la question b), à savoir partir de
2/x = (1/2)x - (3/2)
pour arriver à x²-3x-4=0...
Quand je lis les abscisses des points d'intersection des deux droites je peux observer que je retrouve les même solutions
Quand je lis les abscisses des points d'intersection des deux droites je peux observer que je retrouve les même solutions
Ben heureusement que tu retrouves la même chose...

écriture complètement fausse
x-3/2 veut réellement dire
et pas du tout qui s'écrit (x-3)/2 parenthèses ajoutées obligatoires quand on écrit en texte sur une ligne
sinon l'opération de division "/" étant prioritaire sur la soustraction, elle est effectuée d'abord : 3/2
et c'est cette valeur de 3/2 que l'on retranche de x
et des espaces ou absence d'espaces n'y changent rien du tout
"/" n'est pas une barre de fraction (quelle en serait la "longueur" ???) mais bien une opération de division
(cours de 5ème sur les priorités et parenthèses
et c'est pareil quand on tape des formules dans un logiciel de calcul ou un tableur !!)
bien plus grave car il n'y a même pas l'excuse d'une barre de fraction
x-3*x veut dire qu'on multiplie 3 par x (la multiplication est elle aussi prioritaire par rapport à la soustraction)
et que ce résultat on le retranche de x (ce qui donnerait -2x !!)
ne pas avoir écrit les parenthèses là est donc impardonnable
là aussi, espaces ou pas espaces c'est pareil.
(x-3)*x
et ça fait bien x² - 3x, OK
par ailleurs une erreur de recopie je pense
4/x=(x-3)*x
le x au dénominateur est en trop (il est déja "passé" à droite)
d'ailleurs il n'est plus là la ligne d'après
c'est du cours de cinquième les priorités des opérations !! tu es en première.
tu es tout de même capable de faire la différence entre a*(b+c) et a*b+c !!
Bah ouii!!! la première expression c'est une distribution et l'autre expression on multiplie d'abord a*b on calcul de gauche vers la droite...
c'est interdit les photos de calcul
tu sais et tu peux l'écrire correctement
et d'ailleurs
et c'est pareil quand on tape des formules dans un logiciel de calcul ou un tableur !!
si tu y écris tel que tu l'as fait le tableur ou le logiciel ou la calculette te donneront des résultats faux.
a*(b+c) et a*b+c
on calcul de gauche vers la droite...
non c'est faux
on calcule en suivant les règles de priorités des opérations
c'est seulement en cas de priorités égales que l'on calcule de la gauche vers la droite
(que des additions et soustraction, ou bien que des multiplications et divisons)
a*b+c et c+a*b c'est exactement pareil et dans la seconde on ne calcule pas du tout de la gauche vers la droite.
et a*(b+c) et (b+c)*a c'est exactement pareil et différent de l'autre
tapes donc 2+3*5 = sur ta calculette et
(2+3)*5= tu verras bien la différence !!
Monsieur s'il vous plait depuis le début de cette énoncé je ne comprend pas tout !
Déjà dans la question a où l'on me demande de conjecturer je ne comprend pas
ça je sais on calcul d'abord 3*5 puis on additionne par 2

donc pourquoi penses tu qu'il en serait autrement de x-3*x dans lequel on calculera d'abord 3*x avant de le retrancher de x ??
et donc pour écrire correctement le calcul (qui est tout autre) il faut bien ajouter les mêmes parenthèses que quand on veut calculer (2+3)*5
c'est tout ce que l'on exige d'une écriture correcte des calculs.
ajouter les parenthèses indispensables au bon endroit, le calcul étant incompréhensible car formellement faux en leur absence.
on me demande de conjecturer je ne comprend pas
ici l'observation des deux courbes sur l'écran de la calculette et rien d'autre.

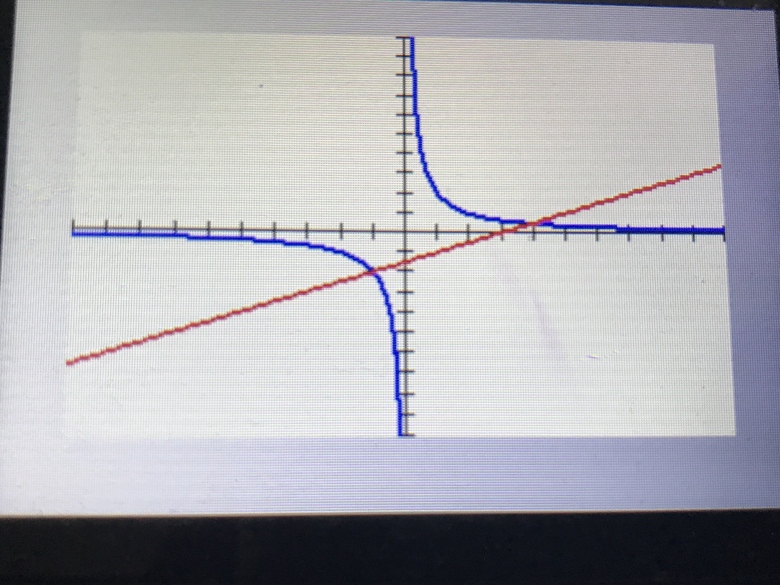 voici pour la 1
voici pour la 1

