Inscription / Connexion Nouveau Sujet
Inverse d'une fonction
Bonjour,
nous sommes en période de confinement et nous devons donc comprendre les cours tous seuls à la maison.
Je travaille sur la dérivée de l'inverse d'une fonction et je ne comprends pas la démonstration:
pour montrer -v'/v² on passe de
[1/v(a+h) - 1/v(a)]/h =[ v(a)-v(a+h)]/[h.v(a+h)v(a)]
Je ne comprends pas vraiment comment on passe de l'un à l'autre et surtout comment les 1/x ont fait disparaître les 1.
Ci-joint la photo de mon cours.
Merci beaucoup d'avoir lu mon message et j'espère des retours positifs.
Justement, si je ne regarde que le 1/v(a+h) - 1/v(a) ça me donne ça et je ne comprends pas comment passer à seulement v(a)-v(a+h)
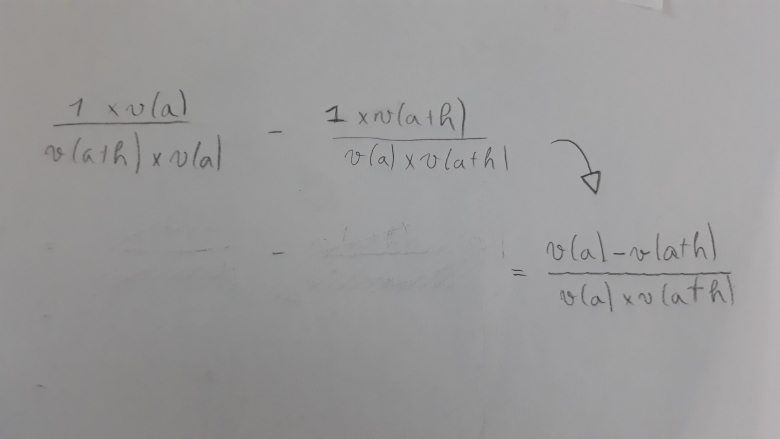
tes dénominateurs sont identiques donc le numérateur de ta fraction finale est égal à la différence des 2 numérateurs de tes fractions
Merci beaucoup pour vos réponses, c'était une question un peu basique mais j'oublie parfois quand on l'a fait il y a longtemps.
Annuler
connectez vous