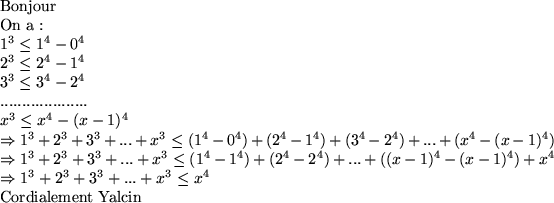.

Bonjour,
j'ai dejà fait une demande d'aide mais apparement mon msg a disparu!!

je bloque sur :
justifier pour tou x1
que 1^3+2^3+3^3+...+x^3x^4
merci bcp (et d'avance) pr votre aide!

*** message déplacé ***

Bonjour Nell, a priori ton message n'a pas "disparu"... la preuve, je l'ai retrouvé en consultant ton profil (clique sur le bonhomme en haut à droite de ton message). Fais de même ou utilise l'option "rechercher mes messages" disponible en bas de cette page la prochaine fois pour retrouver tes messages

Salut , il existe une autre solution :
1^3 + 2^3 + … +x^3 = x²(x+1)²/4 <  x²(2x)²/4 < x^4  cqfd

cette manière me semble plus simple a trouver mais je ne voi pas pourquoi 1^3+2^3+3^3+...+x^3=x²(x+1)²/4

Bonjour

Il faut partir du fait que :



Or ,

On en déduit :


donc :

Bonjour
mais qui vous dit que 1^3+2^3+...+x^3=(1+2+3+...+x)²
il faut démontrer ça aussi, eh oui c'est des maths
Cordialement Yalcin