Je crois que c'est du niveau de terminale mais je vais pas pouvoir t'aider désolé. Il me semble qu'il faut utiliser des intégrales.

Bonjour,

Le point A est un point du plan z = 1

Quelle est l'intersection du cône et de ce plan z = 1 ?
Quelle est l'équation de cette intersection dans le plan z = 1 (origine le point (0, 0, 1) et axes parallèles à Ox et Oy) ?

Bonjour

L'équation cartésienne générale d'un cône d'axe et de centre est :

, avec l'angle entre l'axe et une des génératrices. Cette formule se retrouve en plaçant sur le cône un point M quelconque et H son projeté sur l'axe, et en utilisant la trigo dans le triangle rectangle OHM.

Bref, ici il suffit de calculer avec les coordonnées du point A, et tu as ton équation

Et comment faire pour calculer alpha ? Avec la trigo ?
Désolé si je suis nul sur cet exercice mais c'était à la fin de l'année donc on a pas eu trop le temps de faire des exercices...

Pour ma part, je ne t'ai pas parlé de ni de tan()

Bien sûr tu peux faire comme le propose myself qui connaît la "formule"

Mais tu peux aussi te passer de cette formule et retrouver l'équation comme je te l'ai proposé à 17 h 15

Je l'ai pas compris non plus

Bonsoir à tous

cet exercice m'intéresse ; je réponds d'abord aux questions de Coll message 17 h 15

Bonsoir pppa

Très bien !

En effet l'équation de ce cercle est bien x² + y² = 1

Ce "1" n'est pas n'importe quoi. Ce 1 est le carré de la longueur O'A = OO' = z

Dans le plan z = 1 les coordonnées des points qui appartiennent (au plan et) au cône vérifient donc :

x² + y² = z²

Il est très facile de continuer en prouvant que cette équation reste valable pour tout plan z

et donc... que l'équation de ce cône est x² + y² = z²

merci Coll

2 questions complémentaires pr être sûr que j'ai compris

1/  

On pourrait exprimer la solution de la manière suivante :

La section d'un cône de révolution d'axe vertical Oz par un plan horizontal P de cote z est cercle dont le centre I est

situé sur l'axe Oz.

Soit M (x, y, z) un point de ce cercle. Ce dernier a pour équation dans le plan P : x² + y² = MI².

On a d'autre part dans le triangle OMI : tan alpha = MI/OI = MI/z, alpha étant l'angle MOI. D'où MI = z tan alpha.

L'équation peut donc s'écrire : x² + y² = z²(tan alpha)² (on retrouve l'équation indiquée par myself).

OM est une génératrice du cône et l'angle alpha est constant. Pour calculer la valeur de sa tangente, il suffit d'écrire

que le point A (1; 0; 1) est sur le cône, c'est-à-dire que ses coordonnées vérifient l'équation ci-dessus :

1² + 0² = 1² (tan alpha)², d'où tan alpha = 1.

L'équation du cône est donc : x² +  y² = z².

J'ajoute qu'un cône complet se compose de deux nappes symétriques par rapport à son sommet.

Je suis un peu perdu par toutes vos réponses , en gros c'est quoi la solution de mon exercice et pourquoi ? SVP

Bonsoir

>> David : concentre toi bien sur ce qu'on répondu Coll et Priam (demain, p.e. plus ce soir) ; ils ont expliqué en détail comment on trouve cette équation, mais ça implique que tu  saches comment on détermine l'équation d'un cercle et ce qu'est une tangente (ça je pense que tu sais ) ; sinon tu ne peux pas faire un tel exercice.

>>Priam : merci pr tes ex^plications très claires

Figure dans le plan xOz (l'axe Oy est perpendiculaire à la feuille et est dirigé depuis l'observateur vers la feuille) :



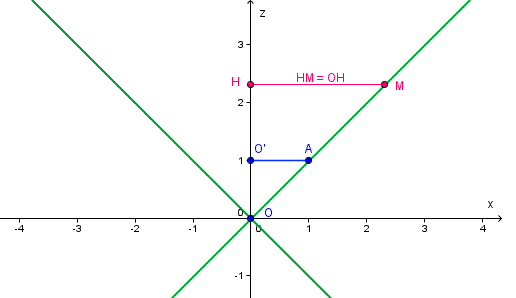
Les lignes vertes sont les intersections des deux nappes du cône avec le plan de la figure.

Un plan z = a coupe l'axe Oz en un point H (O, O, a) et la génératrice OA en un point M
Puisque OO' = O'A (coordonnées du point A) alors OH = HM = a

L'intersection du cône et du plan z = a est un cercle de rayon R
Dans ce plan z = a tous les points du cône ont des coordonnées (x, y , a) qui vérifient
x² + y² = R² = HM² = OH² = a² = z²

Equation de ce cône : x² + y² = z²

bonjour Coll

C'est encore + clair avec un schéma. merci

Si  j'ai bien compris, peut-on dire que les nappes du cône, c'est l'ensemble de ses génératrices ?

Si Priam lit le message, j'espère qu'il aura la gentillesse de répondre à mes questions

C'est bien l'ensemble des génératrices rectilignes qui forme la surface du cône (on dit que c'est une surface réglée).

Comme elles sont de longueur infinie et passent toutes par le sommet du cône, la surface de celui-ci se compose de deux

nappes coniques opposées par le sommet, à la manière d'un diabolo.

Ok merci Priam ; est-ce que tu peux stp répondre à mes questions d'hier soir ; pr ma part, si tu valides, j'en aurai fini avec ce sujet intéressant et qui m'aura appris bcp de choses en peu de tps.

Merci d'avance

Pour déterminer un cône de révolution, il suffit de connaître son axe, son sommet et un point de sa surface.

Au cas où le sommet ne serait pas en O, origine des axes de référence, il pourrait effectivement être commode de faire

un changement de repère pour se ramener au problème précédent. Mais je pense que ce n'est pas indispensable.

Bonjour Priam