Inscription / Connexion Nouveau Sujet
L Île des Mathématiques 3/3


Voici la dernière énigme de cette trilogie. N'hésitez pas à consulter les précédentes énigmes:
Trilogie: L Île des Mathématiques 1/3 et Trilogie: L Île des Mathématiques 2/3
L'Île des Mathématiques s'est développée tellement vite que chaque chemin est devenu une rue importante et les maisons de 8 premiers habitants de l'île sont placés aux carrefours de ce qui est maintenant une ville. Un service de poste est en train d'être mis en place et le bâtiment principal sera construit au même carrefour où habite Nightmare. Le facteur cherche à parcourrir toutes les rues au moins une fois afin de distribuer le courrier. Il part du bâtiment de la poste et y revient à la fin de son parcours.
Quelle est la longueur du plus court parcours lui permettant de passer au moins une fois par chaque rue?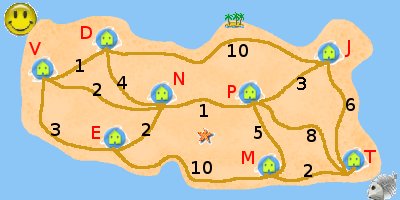
Clôture au plus tôt vendredi soir
Isis



Bonsoir,
J'opte pour la réponse: 66
Severus



 zut en fait j'ai fait pour qu'ils passent une fois par chaque maison!!! mal lu l'énoncé. Je parie que dans ces cas là on peut pas annuler ce qu'on a dit et reproposer qqch ou juste annuler ce qu'on a dit?? je tente ma chance quand même on sait jamais 66km (d'un côté j'espère que je me trompe j'aurais pas de regrets si c'est non)
zut en fait j'ai fait pour qu'ils passent une fois par chaque maison!!! mal lu l'énoncé. Je parie que dans ces cas là on peut pas annuler ce qu'on a dit et reproposer qqch ou juste annuler ce qu'on a dit?? je tente ma chance quand même on sait jamais 66km (d'un côté j'espère que je me trompe j'aurais pas de regrets si c'est non)



 Hello ce soir mon petit orteil droit qui me fait mal m'a dit que le facteur doit parcourir au moins
Hello ce soir mon petit orteil droit qui me fait mal m'a dit que le facteur doit parcourir au moins
* image externe expirée *
++ EmGiPy ++
 La méthode consiste lorsqu'il y a 3 chemins arrivant en 1 point à considérer que le facteur effectue le plus court deux fois (aller-retour), et à le supprimer de façon à ne constituer que des boucles.
La méthode consiste lorsqu'il y a 3 chemins arrivant en 1 point à considérer que le facteur effectue le plus court deux fois (aller-retour), et à le supprimer de façon à ne constituer que des boucles.
Les allers retours sont donc :
V-D : 1km
E-N : 2km
M-T : 2km
P-J : 3km
N-P : 1km
Soit 9 km supplémentaires par rapport au taotal des chemins (57 km).
Le parcours minimum du facteur sera donc de 57 + 9 = 66 km.
Exemple :
N-2-V-1-D-1-V-3-E-2-N-2-E-10-M-2-T-2-M-5-P-8-T-6-J-3-P-3-J-10-D-4-N-1-P-1-N.
2+1+1+3+2+2+10+2+2+5+8+6+3+3+10+4+1+1= 66 km
 La longueur du plus court parcours permettant au facteur de passer au moins une fois par chaque rue est de 66km.
La longueur du plus court parcours permettant au facteur de passer au moins une fois par chaque rue est de 66km.



 Bonjour,
Bonjour,
Réponse : 64 km
Un des chemins parcouru peut être le suivant :
ND-(DV-VD)-DJ-JT-(TM-MT)-TP-(PJ-JP)-PM-ME-(EN-NE)-EV-VN-(NP-PN)
Les trajets entre parenthèses correspondent à des aller-retours.
Afin de minimiser le parcours, ces AR sont effectués sur des distances les plus courtes.
Il a donc été rajouté, à la distance minimale, les 5 trajets:
DV-TM-PJ-EN-NP
En applications numériques :
ND-(DV-VD)-DJ-JT-(TM-MT)-TP-(PJ-JP)-PM-ME-(EN-NE)-EV-VN-(NP-PN)
4+(1+1)+10+6+(2+2)+8+(3+3)+5+10+(2+2)+3+2+(1+1)=64 km
et un rajout de :
DV-TM-PJ-EN-NP
1+2+3+2+1= 9km sur les 55 km minimaux.
Merci pour l'énigme,
Philoux
>Pourrait-on nous donner la "bonne" méthode pour résoudre, sans tâtonner, ce type de pb (théorie des graphes, je crois) ?
A moins que ça "plane" trop haut...
 salut isiss et bonjour à tous
salut isiss et bonjour à tous  :
:
Ca sent le  a plein nez, mais bon allez, je me lance ( j'ai une escuse, c'est une 3 étoiles alors ... )
a plein nez, mais bon allez, je me lance ( j'ai une escuse, c'est une 3 étoiles alors ... ) 
Alors j'ai eu beau chercher moins, après avoir étudiées environ 50 possibilités, je n'ai pas réussi à passer en dessous la barre des 66 km.
J'imagine que l'on peut trouver moins, mais comme je n'ai pas réussi à me mettre dans cette situation, je ne vais pas me lancer à donner un nombre au hasard entre 60 et 66 ... 
Ma réponse est donc la suivante : la longueur du plus court parcours permettant au facteur de passer au moins une fois par chaque rue est de
Envoyer le  !
!
@+
lyonnais

 Voilà qui ressemble beaucoup plus à ce que j'avais imaginé...
Voilà qui ressemble beaucoup plus à ce que j'avais imaginé...
Je pensais à la distance minimale que Tom_Pascal devrait parcourir s'il décidait de rendre visite à tous les habitants de l'île ! Encore un problème d'optimisation.
L'énigme proposée ici est légèrement différente.
Le facteur doit couvrir toutes les rues.
La réponse est .
Voici une démonstration
(car il est bien facile de trouver une solution mais sans démonstration comment savoir avec certitude qu'on tient le minimum):
La somme totale des longueurs vaut .
Sachant qu'il y a 6 maisons qui ne possèdent que 3 routes y menant (carrefours entourés), il faudra, de toute façon, parcourir plusieurs fois les mêmes rues.
Puisqu'on ne peut accéder aux carrefours entourés que par un nombre impair de routes (ici 3), le facteur devra obligatoirement parcourir l'une d'elle dans les deux sens
(j'ai supposé que le facteur distribuait en réalité le courrier simultanément des deux côtés car ce n'est pas précisé dans le texte... mais "le facteur cherche à parcourir toutes les rues au moins une fois" donc je pense que c'est la réponse attendue sinon il n'aurait pas fallu rajouter cette phrase qui va dans le sens contraire. De plus, c'est possible au regard de la densité de la population!  ).
).
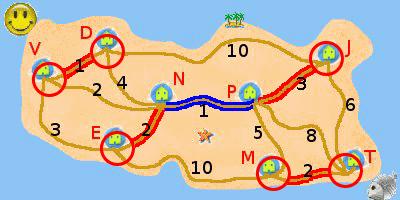
Ensuite pour minimaliser les distances on va choisir pour chaque carrefour de doubler (i.e. de parcourir deux fois) la plus petite longueur et si possible en utilisant la même longueur doublée pour plusieurs carrefours (comme M-T et V-D). On en déduit les quatre rues doublées en rouge.
Maintenant la distance minimale s'élève à 57+1+2+2+3 = avec ces longueurs doublées.
Enfin, si on observe alors ce qu'il se passe en N, départ du parcours, avec la longueur doublée rouge, il y aurait 5 chemins menant à N. Mais à chaque fois que l'on passe par N il faudra y revenir (en particulier pour finir le parcours) donc le nombre de rues qui mènent à N sera nécessairement pair. D'où la nécessité de doubler un chemin supplémentaire et, tant qu'à faire, encore celui minimisant la distance donc le chemin bleu N-P de longueur 1 km.
On peut finalement conclure que la longueur totale du parcours vérifiant les conditions requises sera au minimum de 65 + 1 = .
Enfin, il est aisé avec exactement ces longueurs doublées de trouver un parcours convenable.
Le minimum est atteint et notre énigme résolue ! 



 Bonsoir,
Bonsoir,
la longueur du plus court parcours lui permettant de passer au moins une fois par chaque rue vaut 66



 Bon, alors la plus compliqué déja ...
Bon, alors la plus compliqué déja ...
Pour moi la réponse est 66 km pour le parcourt le plus court ... mais de nombreuses variantes existent (la ptet le pbl ... espérons qu'il n'y en ait pas une plus courte ... lol), même si certaines se ressemblent : cf tableau




 La longueur du plus court parcours lui permettant de passer au moins une fois par chaque rue est de 66km.
La longueur du plus court parcours lui permettant de passer au moins une fois par chaque rue est de 66km.



 Quand on va quelquepart, il faut en revenir. Partant de ce principe simple, quand un carrefour a un nombre impair de routes, l'une de ces routes doit forcément être visitée 2 fois. C'est le cas pour tous les points situés en périphérie de l'île, qui ont tous 3 chemins d'accès. Quitte à passer 2 fois sur la même route, le facteur préférera que ce soit la plus courte :
Quand on va quelquepart, il faut en revenir. Partant de ce principe simple, quand un carrefour a un nombre impair de routes, l'une de ces routes doit forcément être visitée 2 fois. C'est le cas pour tous les points situés en périphérie de l'île, qui ont tous 3 chemins d'accès. Quitte à passer 2 fois sur la même route, le facteur préférera que ce soit la plus courte :
-pour les points V et D, il doublera le trajet DV (1km)
-pour les points M et T, il doublera le trajet MT (2km)
-pour le point E il doublera le trajet EN (2km)
-pour le point J, il doublera le trajet JP (3km)
En fait comme il y a 6 carrefours à 3 routes, on aurait pu s'arranger pour ne doubler que 3 routes (reliant 2 de ces 6 carrefour). Mais cela obligerait à passer 2 fois sur une route de 10 km, ce qui est bien trop long. Cette solution est donc à éliminer, et il faut bien doubler 4 routes pour desservir la périphérie de l'île.
Il reste un dernier problème : comme nous avons choisi de doubler certaines routes qui vont de la périphérie vers le centre (EN et JP), il y a maintenant 5 itinéraires qui convergent en N et P, pour lesquels on se retrouve à présent avec un nombre impair de trajets. La solution est d'en rajouter un sixième en doublant NP (1km).
En conclusion, le facteur va passer 2 fois sur 5 portions de routes qui sont DV, MT, EN, JP et NP. Ces 5 portions totalisent 1 + 1 + 2 + 2 + 3 = 9 km.
Comme la somme des longueurs de toutes les routes fait 57 km, le meilleur itinéraire pour le facteur fera 57 + 9 = 66 km. Bigre c'est une belle tournée ! S'il fait ça tous les jours à vélo, il va avoir de beaux mollets...
Il y a de nombreuses solutions, bien sûr. En voici une, avec de jolies boucles, qui lui permet de repasser régulièrement par le bureau de poste pour recharger ses sacoches :
NE 2
EV 3
VD 1
DN 4
NV 2
VD 1
DJ 10
JT 6
TM 2
MP 5
PT 8
TM 2
ME 10
EN 2
NP 1
PJ 3
JP 3
PN 1
TOTAL = 66 km



 Bonjour,
Bonjour,
En toute conviction, je trouve, pour passer ds chaque rue,
(ou route...), un miminum de 66.
BABA
 Le meilleur chemin que j'ai trouvé est 64 km. si vous voulez le détail, le voici. Je ne doute pas qu'il doit y avoir plus court, mais je suis quand même parvenu à 64 sans trop chercher... et ma méthode n'était pas mathématique mais intuitive ^^
Le meilleur chemin que j'ai trouvé est 64 km. si vous voulez le détail, le voici. Je ne doute pas qu'il doit y avoir plus court, mais je suis quand même parvenu à 64 sans trop chercher... et ma méthode n'était pas mathématique mais intuitive ^^
NP-PT-TJ-JD-DV-VE-EM-MT-TM-MP-PJ-JP-PN-NE-EN-NV-VD-DN
J'éspère ne pas avoir fait d'erreur de calcul...
 bonjour,
bonjour,
j'ai fait de mon mieux, je crois que le parcours le moins court permettant à notre cher facteur de passer au moins par chaque rue est de 66 Km...
en fait j'ai essayé de faire en sorte que :
-le parcours de courte durée doit être supérieur à 57 Km...
-le parcours soit le plus proche de cette valeur...
-les rues passées deux fois soient celles ayant une longueur minimale...
et voilà! en espérant que je ne me suis trompé...
j'ai essayé de faire la chose sans intuition mais je manque vachement de temps!
et 66 Km c'est pas si désespérant pour notre facteur!!
 Le parcours le plus court est constiué des tronçons suivants dans cet ordre:
Le parcours le plus court est constiué des tronçons suivants dans cet ordre:
1 N-D :4
2 D-J :10
3 J-T :6
4 T-P :8
5 P-J :3
6 J-P :3
7 P-M :5
8 M-T :2
9 T-M :2
10 M-E :10
11 E-N :2
12 N-E :2
13 E-V :3
14 V-D :1
15 D-V :1
16 V-N :2
Soit au total 64 km de parcours
 bonsoir,
bonsoir,
le parcours le plus court esr de 27 kilometres en allant d'un cote ou de l'autre.
a plus tard
merci
bonsoir
PAULO



 comme il faut passer par toutes les rues (au moins une fois) la distance minimale à parcourir est de 57 km.
comme il faut passer par toutes les rues (au moins une fois) la distance minimale à parcourir est de 57 km.
Je pense que la longueur du plus court parcours est de 62 km, que l'on peut atteindre de deux (au moins ...) façons :
NVDJTMPNEVDNEMTPJ
NVDJTMENDVENPTMPJ

 Bonsoir à tous je dirai 66km
Bonsoir à tous je dirai 66km
En effet la somme de tous les kilometrages indiqués fait 57,
je le referrai passer par le 1 entre V et D , le 1 entre N et P, le 2 entre N et E, le 2 entre M et T et enfin par le 3 entre J et P.
Sans trop grande conviction, mais pour PLAGIER un certains polytechmars... je vous laisse deviner cette belle phrase de Pierre de Coubertin.
A+, h
 Mes biens chers frères, mes bien chères soeurs...
Mes biens chers frères, mes bien chères soeurs...
REPRENONS ENSEMBLE CE REFRAIN TOUS EN COEUR!!!
Pas de boogie-... Oups, jme suis trompé 
Pour la réponse on s'en fiche mais je pense que c'est 66km, mais je trouve débil de placer une poste en plein milieu comme ca, il faudrais faire en sorte que on puisse...voila quoi...
Oh, et puis flûte, votre facteur, il avait qu'a pas avoir de vélo, il avait qu'a louer un jet privé ca iré plus vite.
Voila une nouvelle enigme que je vous propose:
Qu'est-ce qui est le plus lourd: Un kilo de plume ou un kilo de plomb ?
Attention il y a un piège ! 

@+ les amis
Ma psy vous passe le bonjour 
 Bonjour à tous,
Bonjour à tous,
J'ai calculé plusieurs itinéraires et le plus court que je puisse trouver, c'est 66 Km (Par exemple : N-D-J-P-N-V-D-V-E-N-E-M-T-J-P-T-M-P-N soit 4-10-3-1-2-1-1-3-2-2-10-2-6-3-8-2-5-1...)
Sans trop de conviction quand même...






 Le facteur peut parcourir 66 Km au minimum en faisant
Le facteur peut parcourir 66 Km au minimum en faisant
N-P-J-D-N-E-V-D-V-N-P-J-T-P-M-T-M-E-N. Mais il y a peut être plus court car je trouve qu'il revient souvent sur ses pas...



 salut.
salut.
je dirais 64 mais sans grande conviction  .
.
 Je n'ai pas trouvé mieux qu'un chemin de longueur 66 km pour passer au moins une fois par chaque rue.
Je n'ai pas trouvé mieux qu'un chemin de longueur 66 km pour passer au moins une fois par chaque rue.
Merci à tous pour votre participation. La réponse attendue était 66 km. J'ai préparé une petite explication pour ceux qui n'étaient pas sûrs d'avoir trouvé l'optimum et pour ceux qui voudraient connaître une autre méthode que le tâtonnement.
Première remarque: l'importance de l'emplacement de la poste est absulement nulle dans ce problème. À partir du moment où on a trouvé un circuit fermé, on peut interrompre ce circuit à n'importe quel carrefour.
Vous avez sûrement déjà essayé de dessiner des petites figures géométriques "sans lever le crayon du papier". Vous savez aussi très probablement que pour que ceci soit possible il faut compter le nombre de traits par croisement. S'il y a 0 ou 2 croisements comptant un nombre pair de traits le dessin est possible. Pour que le dessin se termine au même point où il a commencé il faut que tous les croisements aient un nombre pair de traits.
Ce même principe est appliquable à notre problème du circuit du facteur. Sur cette île il y a 6 croisements avec un nombre impair de chemins. Pour qu'on puisse dessiner l'île sans lever le crayon du papier en commençant et en finissant en N il faut dédoubler certains chemins pour que tous les croisements aient un nombre pair de chemins. Les chemins à rajouter doivent avoir une longueur totale minimum.
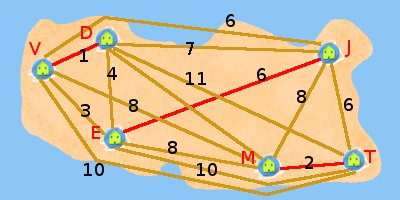
Comment trouver les chemins à rajouter? Je construis un plan de l'île où je mets tous les croisements de degré impair et où entre chaque paire de croisements je mets une rue imaginaire dont la longueur est celle du plus court chemin entre les deux croisements sur le vrai plan de l'île. Par exemple la droite EJ représente le plus court chemin de E à J qui est ENPJ de longueur 6km. Sur cette nouvelle carte je dois choisir 3 chemins de sorte que ces 6 croisements soient arrangés par paires et que la somme des longueurs de ces 3 chemins soit minimum.
De cette manière je trouve que les chemins à parcourrir à double sont VD, EJ (en réalité ENPJ) et MT. Ces chemins ont ensemble une longueur de 9km à rajouter à la somme des longueurs de tous les chemins qui est 57km. Il y a ensuite une quantité énorme de parcours de 66 km assez faciles à trouver.
Isis
 cool, j'ai eu bon ...
cool, j'ai eu bon ... 
J'avais des doutes, parce qu'a chaque fois que je faisait une tentative, je tombais toujours sur 66 !
Mais en fait, j'ai eu raison de donner ma réponse.
Merci pour l'énigme isiss et @+
lyonnais

 bonjour,
bonjour,
j'ai suivi le meme raisonnement qu Eldamat et Pietro . On pouvait facilement comprendre certes en n'interpretant pas l'énoncé a votre maniere que le facteur devait aller porter les lettres dans les maisons marquées sur le plan . De plus , dans ce cas , notre solution de 27 km est bonne .
je pense que nous méritons donc un smiley et dans ce cas vous pouvez reprendre votre poisson qui ne manquera pas de servir dans l'avenir , meme, pourquoi pas ? à nous memes.
En tout cas merci de me lire.
PAULO
Ps: peut-etre ce jour n'y avait-il-pas de courrier pour les campeurs?
bon dimanche
Alors là je suis désolée, la donnée est claire et si vous ne la lisez pas attentivement ce n'est pas de ma faute. J'ai bien dit que la petite île est devenue une ville et que les maisons sont des carrefours. J'ai dit encore deux fois que le facteur cherchait à passer par toutes les rues et non pas par tous les carrefours .
Peut-être que depuis la première énigme de la trilogie vous vous attendiez déjà à avoir un épisode traitant le classique problème du voyageur de commerce alors que j'ai préféré celui du facteur chinois. 
Isis
Tu penses vraiment paulo, qu'avec la phrase de l'énoncé "Le facteur cherche à parcourir les rues au moins une fois afin de distribuer le courrier.", on pouvait interpréter comme tu l'as fait?
Remarque que quand Isis a posé sa question dans la partie du site seulement accessible aux "poseurs d'énigmes", j'ai failli faire la même erreur, mais en relisant l'énoncé calmement, c'était clair.




 Non je suis d'accord avec les correcteurs l'énoncé était clair c'est nous qui avons mal interprété!!! la preuve c'est qu'en relisant (ce que je devrais avant de poster plutôt qu'après, lol) je me suis rendu compte de mon erreur!!! Donc Paulo non nous ne méritons pas de smiley, mais c'est pas grave le mois prochain je ferais bien attention au énoncé (ce mois ci aussi bien sûr
Non je suis d'accord avec les correcteurs l'énoncé était clair c'est nous qui avons mal interprété!!! la preuve c'est qu'en relisant (ce que je devrais avant de poster plutôt qu'après, lol) je me suis rendu compte de mon erreur!!! Donc Paulo non nous ne méritons pas de smiley, mais c'est pas grave le mois prochain je ferais bien attention au énoncé (ce mois ci aussi bien sûr )
)



D'accord avec eldamat, qui est d'accord avec les correcteurs, et qui est peut-être d'accordéon avec des amis musiciens.
J'ai lu et cru comprendre trop rapidement l'énoncé. Le passage " toutes les rues " ne m'avait pas frappé.
Je me suis ausssi rendu compte de mon erreur peu de temps après : il faut toujours lire ( et relire ) l'énoncé très attentivement.
@+ pour de nouvelles énigmes.

Bonjour 
>>Pietro:
Où trouves-tu des images similaires à celle que tu poste à chaque énigme ? (ci-dessus). C'est rigolo, et d'ailleurs c'est grâce à ce logo que je connais ton pseudo, enfin il y a certaine personne dont je ne fais pas très attention mais toi je m'en souviens en le voyant 
J'ai beau me servir de google je n'en trouve pas 
Merci 
Kevin
 :)
:)



Salut infophile et les autres
Je vais révéler ce grand secret. 
J'utilise un générateur de smileys qu'on trouve ici :![]() (il faut s'inscrire - avoir un compte pour pouvoir l'utiliser)
(il faut s'inscrire - avoir un compte pour pouvoir l'utiliser)
Kid Paddle se trouve dans un des centaines ou milliers de smileys disponibles. Bon amusement à l'utilisation de ce générateur.

 est trop !
est trop !



 Hey c'est également le site ou je me procure mon petit corbeau fana d'ordinateur!
Hey c'est également le site ou je me procure mon petit corbeau fana d'ordinateur!
C'est un très bon générateur de smiley et pour ma part je ne suis pas inscrit!
++ EmGiPy ++
 Il est vraiment super ton site, Piétro!!!...Et puis, c'est vraiment sympa de nous avoir livré ton secret.
Il est vraiment super ton site, Piétro!!!...Et puis, c'est vraiment sympa de nous avoir livré ton secret.
T'es vraiment "trop".
NF2



 > merci à pied_trot (en référence au challenge 94 de puiséa (Non d'un âne
> merci à pied_trot (en référence au challenge 94 de puiséa (Non d'un âne  ) pour le site.
) pour le site.
Sympa
Philoux
>>Pietro
Je sens que pour les prochaines enigmes, on pourras admirer les mascottes des uns et des autres 
Personnelement, pour l'instant je n'en ai pas trouvé un qui me plaise vraiment, mais je pense également que je n'ai pas su exploiter toutes les fonctionnalités du générateur de smiley. En effet je vois pas mal de monde qui ont des smileys à leurs effectifs, alors que moi je me contente d'explorer leurs pages pour en trouver un qui me convient...
Je me demande comment il est possible d'en créer un 
Merci pour la révélation de ton précieux secret 



Infophile, tu as bien fait de me poser une bonne question 30 cm plus haut. C'est avec plaisir que j'y ai répondu, je savais que ça allait intéresser du monde de connaître mon soi-disant secret.
Je me réjouis à l'idée de voir bientôt des réponses plus colorées aux énigmes. Kid P se sentira moins seul, quoique il ne l'était pas, voir EmGiPy, qui connaissait aussi l'existence de ce site, et son corbeau, Razibuszouzou et ses Tintin et milou.
D'autre part, moi aussi je n'ai pas encore essayé de fabriquer moi-même une mascotte. Peut-être qu'un autre membre nous donnera bientôt des explications dans ce sens .
A bientôt, pour de nouvelles aventures énigmatiques.
Nombre de participations : 0
Temps de réponse moyen : 37:36:16.



