Inscription / Connexion Nouveau Sujet
Le lanceur de javelot : exo compliqué
Bonjour...
Je reprend les cours vendredi :s et j'ai toujours un LONG exo de maths ou je bloque complétement. Je ne comprend rien.
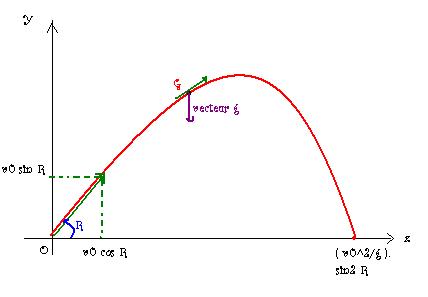
Soit O le point de lancer considéré pour simplifier au niveau du sol(c'est pas trop simple pour moi :s 
) j un vecteur unitaire vertical orienté vers le haut et v0 le vecteur vitesse communiqué au javelot par le lanceur.
O, j et v0 (vecteur) définissent un plan dans lequel on choisit le repère orthonormal direct (O,i,j)
On appel (je sais pas moi! 
un truc ) R l'angle orienté (i;v0) et on prend l'instant du lancer pour origine des dates.
On assimile le javelot à un point matériel G qui, une fois lancé, est soumis à une seule force: son poids P = m.g
On admet que le mouvement de G de coordonnées ( x(t) ; y(t)) sur chacune des directions horizontale et verticale est donné par les équations horaires:
x(t) = (v0 cos R) t
y(t)= -1/2 gt2 + (v0 sin R) t
Enfin les questions
1. Déterminer les coordonnées (x' (t) ; y'(t) ) du vecteur vitesse V(t), puis celles du vecteur accélération a(t), dérivées des coordonnées du vecteur vitesse.
Vérifier que V(0) = v0 (en vecteur :s ) et que, pour tout t supérieur ou égal à 0 :
a(t) = -g j (a et j vecteur)
2. En éliminant t entre les deux équations horaires, démontrer qu'une équation de la trajectoire du point G dans le plan (O, i, j) est:
y = -1/2 (g/v02cos2R) x2 + (sin R/ cos R) x (trop compliqué tout ca:s)
Quelle est la nature de cette trajectoire?
3. Déterminer alors l'abscisse du point d'impact du javelot en fonctionde v0, g et R .
4. (derniere question, enfin!) Déterminer la valeur de R rendant maximale cette abscisse et conclure.
Je sais pas vous, mais moi j'ai rien compris! j'ai essayé de faire cette exercice, mais en vain! il y'a trop de lecon qui rentrent en jeu :s et j'y arrive vraiment pas! donc svp aidez moi, svp
Bonjour,
En ne faisant pas de discours inutiles mais en se concentrant bien sur les questions, je t'assure que cet exercice n'est pas long.
Où en es-tu ? Quelles sont tes premières réponses ?
donc pour la premiere question j'ai dit que V0 avait pour coordonnées : x = v0 sin R et y = v0 cos R (en me basant sur la figure ci dessous)
et pour le vecteur d'accélération je fais la dérivée de x et de y :
x' = v'0 . sin R + sin' R * v0
Non. Il y a des erreurs
Le beau schéma suppose une résistance de l'air, absente de ton problème. Mais c'est presque cela.
Les dérivées de x(t) et de y(t) sont à prendre par rapport à t
De même ensuite les dérivées de x'(t) et y'(t) pour l'accélération
R est une constante de même que sin(R) et cos(R)
mais pour dériver x(t) et y(t) il faut decomposer car il y'a des multiplications et tout... je sais pas :s
On multiplie par une constante... donc, aucune difficulté (il n'y a pas à prendre les dérivées de sin(R) ni de cos(R) qui sont des constantes pour une direction de lancer donnée)
Non,
x'(t = 0) = v0.cos(R)
y'(t = 0) = v0.sin(R)
et c'est tout...
Ce sont bien les coordonnées du vecteur v0 juste à l'instant du lancer (t = 0)
merci et donc V(t) ( v0.cos(R), v0.sin(R) )
et a(t) ( v0'+cosR . cos'R . v0 ; v0'.sinR + sin'R. vO)
et pour Vérifier que V(0) = v0 , on dit que sin (R) et cos (R) représentent des constantes, et on sait que vecteur v0 ( v0.sin R ; v0.cos R)
donc V0 = v0
Les composantes du vecteur accélération en fonction de t ne sont pas correctes.
Faut-il que je répète que sin(R) et cos(R) étant des constantes il n'y a pas à dériver par rapport à ces coefficients ?
Nous avons écrit les composantes du vecteur vitesse pour t = 0
mais ces composantes changent avec le temps (sinon le mouvement serait rectiligne et uniforme)
Quelles sont les composantes de v(t) en fonction de t ?
Ce sont ces composantes qu'il faudra dériver par rapport à t pour avoir les composantes du vecteur accélération.
Il m'arrive de comprendre la solitude de certains profs de physique.
1)
x(t) = (v0 cos(R)) t
y(t)= -(1/2) gt² + (v0 sin(R)) t
x'(t) = Vo cos(R)
y'(t) = -gt + (v0 sin(R))
x''(t) = 0
y''(t) = -g
vecteur v(t) : (Vo cos(R) ; -gt + (v0 sin(R)))
vecteur a(t) : (0 ; -g)
vecteur v(0) : (Vo cos(R) ; -g*0 + (v0 sin(R)))
vecteur v(0) : (Vo cos(R) ; v0 sin(R))
vecteur a(t) : (0 ; -g) (pour t >= 0)
vecteur a(t) = -g vecteur j
-----
2)
...
La piste est simple :
extraire t de l'équation horaire x(t) = ...
et reporter sa valeur dans l'équation horaire y(t) = ...
C'est tout !
re.
1/ On dérive par rapport au temps t
donc v0' et sin' R sont nuls
x(t) = v0cosRt => x'(t)=v0cosR
y(t) = -1/2gt^2 + v0 sin R t => y'(t) = -g t + v0 sinR
et comme le repère est fixe, on peut redériver pour obtenir les composantes du vecteur accélération
x'(t) = v0 cos R => x''(t) = 0
y'(t) = -g t + v0 sin R => y''(t) = -g
2) On doit exprimer t en fonction de x et reporter son expression dans celle de y pour trouver l'équation d'une parabole . Seulement, je ne sais pas comment appliquer cela. Pouvez vous m'aider?
3) y=0 à l'impact mais je ne sais pas comment répondre à la question
4) 2sin R cos R = sin 2R qui est maximum pour 2R = /2 ou R = /4
pouvez vous m'aider?
x(t) = (v0 cos R) t
y(t)= -1/2 gt2 + (v0 sin R) t
De la première tu déduis que
t = x(t) / (v0 cos R)
Tu reportes cette valeur de t dans la deuxième et tu trouves ainsi une expression de y en fonction de x
t = x(t) / (v0 cos R)
y(t)= -1/2 gt^2 + (v0 sin R) t
donc y(t) = -1/2 g (x(t) / v0 . cos R) 2 + v0. sin R . x(t) / (v0 cos R)
y = -1/2 (g/v0^2cos^2R) x^2 + (sin R/ cos R) x
cela est suffisant pour la démonstration??
ensuite on dit que y est l'équation d'une parabole, donc la trajectoire est parabolique. Ca se dit?? est ce correct?
Oui c'est cela.
Pour la question 3 : quelles sont les deux valeurs de x pour lesquelles y = 0
Une première valeur x = 0 ; on retrouve la position du javelot au départ
Une deuxième valeur x = ... qui est celle du point d'impact
en factorisant par x dans l'équation de la parabole je trouve:
x = 0
ou x = - (sin R/cos R) * - [ (2 v0 2 cos 2R) / g ]
y'a pas un moyen pour simplifier?
merci beaucoup pour tout!
svp une derniere question: la valeur de R rendant maximale cette abscisse:
on dit que ; 2sin R cos R = sin 2R C'est maximum pour 2R = pi/2 ou R = pi/4
est ce cela? si oui, que peut on en conclure??
Bonjour,
Tu as très bien terminé : en effet cette manière de faire le calcul avec sin(2R) est bien commode pour trouver l'angle qui permet la portée maximale (en absence de résistance de l'air et, pour les javelots modernes, en l'absence de portance très élaborée)
Bonjour,
Je me permets de poster ici pour un problème sur cette exercice:
je n'arrive vraiment pas à comprendre la question 4) et je ne vous suis vraiment sur votre démarche de réponse pour cette même question: en effet comment pouvez-vous extraire sin2R sans tenir compte de (v0^2/g) sinon j'arrive à vous suivre sur les formules de trigo
Donc pouvez-vous m'éclaircir la chose?
PS: pour la 3) je n'ai pas fais comme vous mais j'ai plutôt fais un discriminant qui me semble plus présentable et mieux explicite mais je trouve la même chose que vous bien sûr c'est-à-dire 0 et (v0^2/g)sin2R
Merci encore pour votre aide bénévole
Bon après une bonne dizaine de minutes de réflexions, j'ai pu enfin apporter une réponse à ma propre question :p. J'ai donc réussi à répondre à la question 4) mais à ma façon...
Donc voici ma réponse si cela peut aider (j'espère):
on a donc (v0^2/g)sin2R donc je me suis dis après réflexion que pour la période qui nous concerne on dira que v0 et g sont constants au cours du temps. Ainsi on s'intéresse exclusivement à sin2R.
Je vais donc dériver sin2R afin de savoir en quelle valeur de R (v0^2/g)sin2R est maximal:
(sin2R)' = cos2R
Donc les valeurs charnières sont: cos2R = 0 donc 2R = pi/2 ou 2R = -pi/2
Soit R = pi/4 ou R = -pi/4
Or pi/4>0>-pi/4
Ainsi en R = pi/4 (=45°) cette abscisse est maximale
Pouvez-vous vérifier et me dire si ma démarche est juste et que conclure sinon?
Merci encore.
Tu connais sans doute l'une des maximes les plus connues des Shadocks : "Pourquoi faire simple quand on peut faire compliqué ?"
Pour moi une démonstration est d'autant plus "présentable" qu'elle est simple, élégante.
Ce n'est pas ton genre apparemment...
Mais tu finis par trouver le bon résultat.
Méfie-toi cependant pour les examens et concours où il est préférable de ne pas perdre de temps et où une solution courte est préférée à une solution inutilement longue.
Annuler
connectez vous