Inscription / Connexion Nouveau Sujet
Le Nombre d'or
Bonjour tout le monde jé un exo à faire, mais le nombre d'ore jamais entendu parler?
Jme suis renseigné un peu, mais je ne vois toujours pas:
Voici la Première Partie de mon exercice:
-Déterminer la valeur 
On pourra prendre AB=x et BC=1
En déduire la valeur de son inverse, celle de  -1/
-1/
Merci d'avance...........
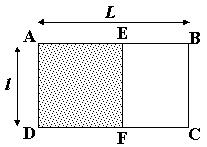
A noter aussi que ABCD est dit "rectangle d'or" lorsqu'ayant tracé le carré intérieur AEFD on a AB/BC = BC/EB
Heu je c qu'il est déja tombé, mais je ne crois pas que ce soit la même consigne, je regarde ......... quand même............
Non dsl je n'est rien trouvé de ce qui correspondait à mon exo?!
oui mais je l'a connais cette valeur, la question posée au dessus disait; Déterminer la valeur de  on pourra s'aider de AB=x et BC =1 ???
on pourra s'aider de AB=x et BC =1 ???
Donc je c pas si je dois la donnée comme ça ou utiliser les donnés qu'ils me donnent? sachant qu'avec les données je trouve x/1=1/x-1
De l'équation x/1=1/x1 , on obtient l'équation (x/1)2-x/1-1=0 dont la solution est x/1 =  ???
???
Bonjour vendredi j'ai eu un DM de maths sur le nombre d'or c'était un test surprise puvez vous me le corrigez afin d'évaluer ma réussite sur ce test ( il a été repris sur le livre ).
A/ Quelques calculs avec le nombre d'or
1. En utiliant votre calculatrice, donner une valeur arrondie de phi à 10-(exposant)3 près.
2. Toujours avec votre calculatrice donner une valeur arrondie de phi(au carré) à 10-(exposant)3 près, puis conjecturer une relation entre phi(au carrée) et phi
3. On se propose de vérifier la conjecture établie à la question 2.
a.Montrer que phi(au carrée)=3+racinede5/2
b.Calculez phi+1 et vérifiez que phi(au carrée)=phi+1 ( relation R)
4.a. En utilisant la relation R, établir que phi(au cube)=phi(au carrée)+phi, puis que phi(au cube)=2phi+1
b. Démontrer que phi( au 4)=3phi+2
c.Démontrer une relation entre phi(au 5) et phi.
B/ Rectangle d'or
On appelle rectangle d'or un rectangle dont le quotient de la longeur par la largeur est égale à phi.
On suppose que le rectangle ABCD est un rectangle d'or
On pose AB=l
1. Exprimer la longeur AD en fonction de l et de phi.
2. On enlève au rectangle ABCD le carré ABEF.
a. Montrer que EF/FD=1/phi-1
b. En utilisant la relation R, montrer que phi(phi-1)=1, puis que 1/phi-1=phi
c.Que peut-on en déduire pour le rectangle coloré FDCE ?
C/ Construction d'un rectangle d'or.
Cette construction semble due à Euclide.
1. Construire un carrée ABCD tel que AB=4cm. Soit I le milieu de AB. Le cercle de centre I passant par C coupe la demi-droite AB en P. Construire enfin le rectangle APQD.
2.Vérifier que les rectangles APQD et BPQC sont des rectangles d'or.
Merci d'avance





