Inscription / Connexion Nouveau Sujet
lecture graphique des paramètres d'une loi binomiale
Bonjour, j'ai une question probablement toute bête, sur la représentation graphique d'une loi binomiale (photo jointe à ce post)
Il est demandé de lire graphiquement les paramètres de la loi binomiale.
Je comprend bien qu'on a représenté p en fonction de n, et qu'il s'agit de relever n et p.
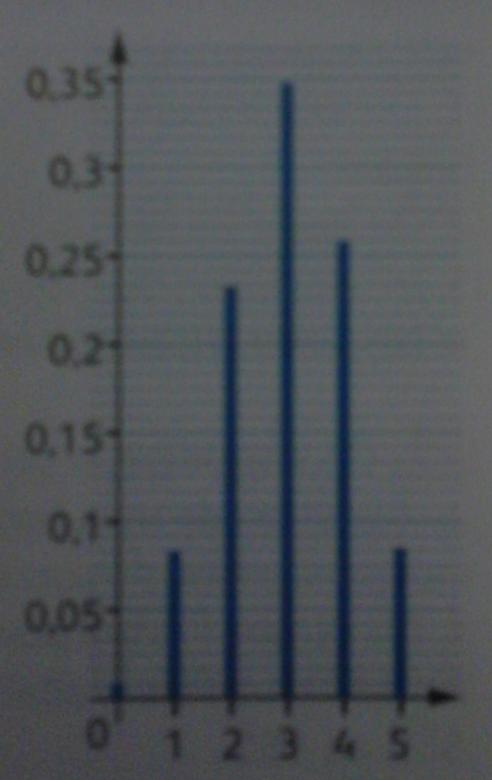
Je pense que n est égal à 5 mais je ne vois pas comment relever p, puisqu'on a une valeur de p différente pour chaque valeur de n (et c'est normal)
Il est bien précisé par lecture graphique, donc a priori on a même pas besoin de passer par des calculs. Pourriez-vous m'indiquer comment lire la valeur de p svp?
Merci
Bonjour romainromain
que sais-tu sur la loi binomiale de paramètre et notamment que vaut
si
représente un va qui suit une telle loi ?
Je connais la formule qui dit que p(X=k)= (k parmi n) 
pk(1-p)n-k et qui permet de trouver la probabilité d'obtenir k succès sur n épreuves réalisées
je pense que ça représente les différentes probabilités pour chaque valeur possible de k
Mais ce n'est pas la même chose que de trouver la probabilité p qui est le paramètre de cette loi, non?
Bonsoir,
une bonne façon est de relever les probabilitéspour chaque possibilité :
0 0.01
1 0.07
2 0.23
3 0.35
4 0.26
5 0.08
vérifier si la somme des probabilités vaut bien 1 : Ce qui est bon, mais qu'il faut toujours vérifier
chercher ensuite l'Espérance par
finalement E=np et ici n=5 d'où p cherché
on trouve p=0.6
Aider un eleve ne consiste pas à faire l'exercice à sa place.
Il dira probablement merci mais qu'aura-t-il appris ?
Intervenir ainsi alors qu'une discussion est en cours n'est pas tres bien venu.
@ alb12 : Vous avez (presque) raison,
mais plus de 3 heures sans réponse à sa dernière question et sans piste, le demandeur peut se décourager...
J'ai posé une démarche logique,
suggéré un calcul, dit comment l'utiliser et donné un résultat final pour conforter les propres calculs que doit développer le demandeur.
Cela me parait d'une pédagogie acceptable et recommandable.
je pense que ça représente les différentes probabilités pour chaque valeur possible de k
moi je me serais contente de relancer en lui demandant d'ecrire les probas
Merci
Le calcul pour l'ésperance est bien 0*001+1*0,07+2*0,23+...+5*0,08 = 3,02?
Pour ce qui est de la méthode avec n*p j'y avais pensé mais justement je ne savais pas comment trouver l'espérance à partir du graphique. D'autant que dans le sujet il est indiqué de lire graphiquement p... (sous entendu sans calculs) ce qui ne m'a pas aidé
Je ne faisais que reprendre les valeurs proposées par vham.
Du coup pr p(X=0) vous liriez quoi? 0,0083333 (qui correspond à 0.05/6 du fait des 6 gratudations)? c'est un peu compliqué que ce soit 6 graduations et non 5 
Au delà de la précision de la lecture, sur le principe vous diriez que mon calcul du post du 15 à 20h53 est bon?
Bonjour, surtout que P(X=0) n'entre dans l'espérance que par les approximations pour que la somme des probabilités égale 1
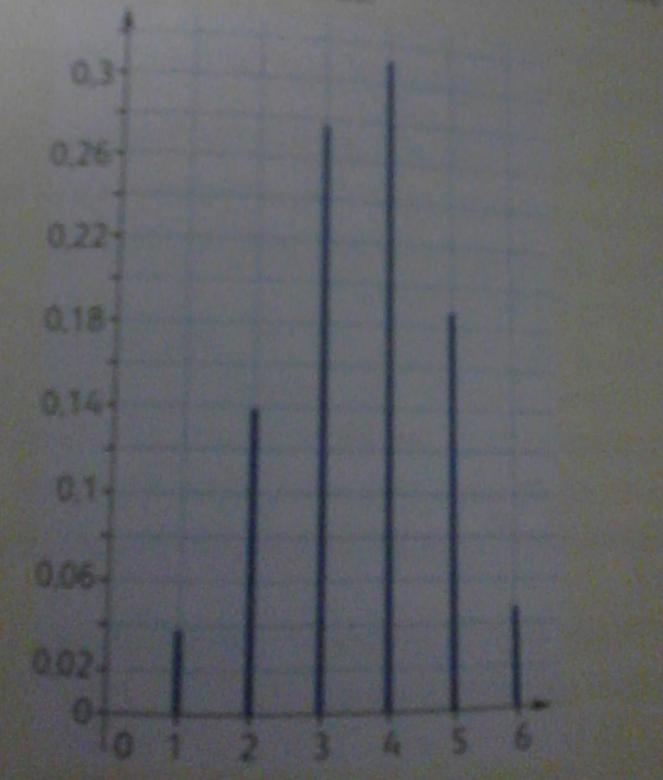
Bonjour, le sujet étant un peu bizarre, je me permets d'ajouter un exercice très très similaire pour vérifier si j'ai compris (bien que là aussi la lecture précise soit des différentes probabilités soit difficile...)
Ici sur la photo on lis n=6
On peut faire le calcul de l'espérance comme suit:
E(X)= 1*0.04+2*0,14+3*0,28+4*0,31+5*0,19+6*0,05=3,65
or E(X)=n*p
d'ou p=E(X)/n=3,65/6=0,608
Vous pensez que c'est correct?
Merci
Bonjour,
La somme des probabilités lues est 1.01 donc erronnée
Il faut qu'elle soit 1.00 sinon ennuis dans les calculs ultérieurs !
D'accord je comprend et tacherai de m'en souvenir. Dites moi vu la précision de la lecture pour les deux graphiques en question, la lecture reste approximative et on fait en sorte de retomber sur 1,00... Peut être que les exercices ne sont pas top, c'est un peu du 'bouinage' non?
Une probabilité ne requiert pas une grande précision. C'est une estimation d'un futur...Mais toujours 1 exactement pour la somme des événements possibles.
Annuler
connectez vous