Inscription / Connexion Nouveau Sujet
Lecture graphique sur les dérivations
Bonjour, j'aurai besoin d'aider pour mon devoir de maths sur la dérivation et je n'arrive pas comprendre. Une aide me serais d'un grand bien.
Exercice n°2:
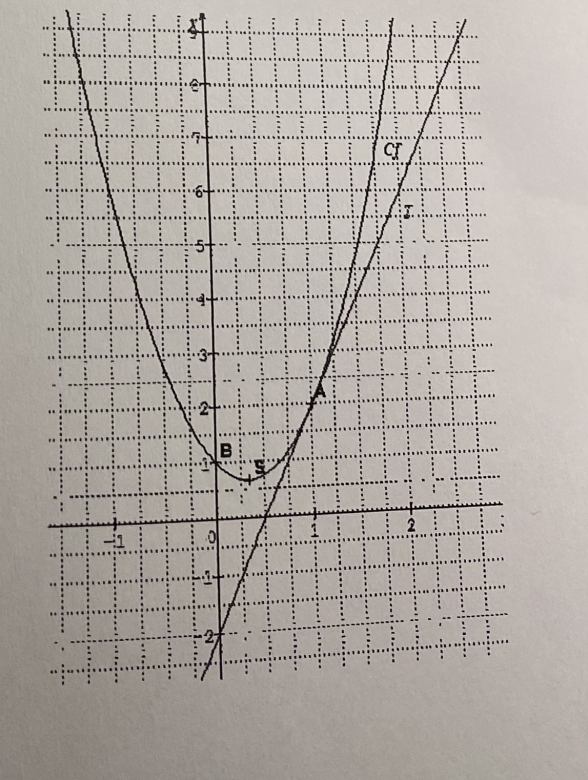
Une fonction est définie sur R par f(x) = ax-+ bx+ c.
La courbe représentative C de la fonction / est représentée ci-contre.
On a placé sur sa courbe représentative les points A(1;2), B(0;1) et le sommet S de la parabole. Soit T la tangent à C, en A.
1. A l'aide des renseignements de l'énoncé et du dessin,
Déterminer f(0), f(1)et f '(1)
2. Justifier que c = 1
3. Montrer que les nombres a et b sont solutions du système :
{a+b=1
{2a+b=4
En déduire les valeurs de a et b.
4. Calculer l'équation réduite de la tangente T à C au point d'abscisse -1. Placer cette tangente T sur le graphique.
attention, cette image n'est pas autorisée, je la laisse pour cette fois, mais tu devras recopier tes recherches et tes calculs dorénavant
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
f(0) et f(1) je suis OK
le coefficient directeur de la tangente est faux, car regarde ! B n'est pas sur la tangente, il faut refaire
pour la 2) je suis d'accord
Tes réponses pour et
sont bonnes.
Ta réponse pour est fausse.
est la pente de la tangeante à la courbe au point d'abscisse 1 (autrement dit A).
Ton idée d'utiliser la formule de la pente est bonne, mais tu as pris de mauvaises valeurs, il faut prendre 2 points qui sont sur la tangeante.
Je te suggère A (évidemment) et puis un deuxième point que je vais appeler C facile à lire et qui a pour coordonnées (2 ; 6).
Après calcul tu devrais obtenir .
Voici le détail :
*****modération > merci de laisser faire l'élève ****
Bonjour Howard75
Notre philosophie est de guider l'lève, mais pas de lui donner les réponses.
Je te remercie d'en tenir compte désormais 
Tu as aussi bon à la question 2) mais je préciserais pourquoi.
C'est parce qu'en utilisant les coordonnées du point qui se trouve sur la courbe
de la fonction
, l'expression de la fonction qui est
donne :
Pardon malou ! 👍
Je pensais que lui expliquer l'origine de son erreur lui serait plus utile étant donné qu'il/elle a déjà eu l'idée de la bonne méthode pour résoudre la question qui lui était posée.
Excuser moi je suis nouvelle , je n'arrive pas encore à m'y faire
Pour la question 3 j'ai mis ça
Le système d'équations suivant peut être résolu pour trouver les valeurs de a et b :
a + b = 1
2a + b = 4
En soustrayant la première équation de la seconde, nous obtenons :
a = 3
En remplaçant a dans la première équation, nous obtenons :
3 + b = 1
Donc, b = -2
Les valeurs de a et b sont donc a = 3 et b = -2.
Bonjour,
juste en passant
Ok pour la deuxième partie de la question 3
mais il manque la première partie de cette question
montrer que ce n'est pas résoudre
c'est à partir des données (f(0) f(1) f'(1)) obtenues dans les questions précédentes, obtenir ces équations
Howard75 t'a montré en détail comment, à partir de f(0) = 1 obtenir la valeur de c
tu l'avais fait sans en être peut être complètement conscient
pour obtenir les équations de la question 3 c'est "du même genre" avec f(1) et f'(1)
Donc si j'ai bien compris..
Pour a + b = 1
Je fais :
a (1)^2 + b(1)+c =1
Puis pour 2a+b = 2 a(2)^2+ b(2)=4




