Inscription / Connexion Nouveau Sujet
Les angles orientés, Aiiiiiiiiiide.
Salut , je me suis bloquéééééééééééébsur cet exercice , voici l'enoncé, soient 
,1 et A, 3points distincts d'un cercle 
de centre w, Soient C1 et C2 deux cercles passant par A de centres respectifs et 1et qui se coupent en un point P. Ces deux cercles coupent respectivement en S et S1. Montrer que [1] est la mediatrice du segment [AP], c'est une question extrêmement claire. 2) Montrer que ,S1 et P sont alignés, je me suis bloqué ici, je demande votre aide...merci d'avance
Bonjour,
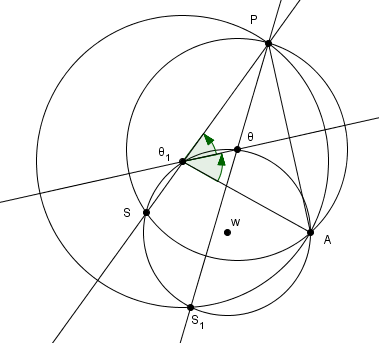
la première question implique une égalité d'angles (orientés)
et donc ...
(avec la condition de cocyclicité sur les angles bien connue, cours, alias "angles inscrits" en version non orientée)
Qla première question implique que que ((teta1,p);teta1,teta) =(( teta1,a);teta1,teta) , donc ces points sont cocycliques, C'est la premiere idée?
"donc ces points sont cocycliques" ??? quels points ???
non.
on sait (par construction) que les points , 1 S et P sont cocycliques (sur )
donc (1; 1S) = (A; AS) mod 
c'est cela la cocyclicité dont je parle
d'autre part (1P; 1) = (
1A); 1) (question 1, avec le signe correct)
et "du même genre" (je n'avais donné qu'un indice, pas tout dit !) avec w médiatrice de AS :
donc (S; AS) = - (A; AS)
en mettant ces trois relations ensemble on obtient (1S; 1P) et donc l'alignement
J'ai bien utilisé cette cocyclicté depuis mes premieres essais mais je n'ai pas remarqué que Wteta med de As pourtant c'était visible , bravoooooooooooo monsieur, l'exercice est long et je demanderai votre aide si j'aurais un problème, mais j'ai une question, comment je peux posséder la capacité de découvrir les astuces en géométrie ? Comment je peux avoir un chemin claire à suivre dans mon cerveau ?
ici avec un dessin et en cherchant un peu on "voit" les angles conjecturés supplémentaires :
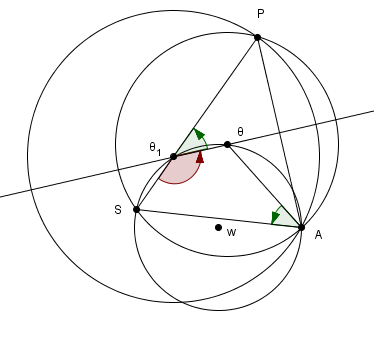
et il ne reste plus qu'à chercher des relations faisant intervenir ces angles par une "chasse aux angles"
de nos jours, un logiciel de géométrie permet de faire facilement des conjectures, qu'il ne reste plus qu'à démontrer "traditionnellement"
l'existence des questions précédentes peut mettre sur la piste
ici la médiatrice de la question précédente fait immédiatement penser à "symétrie" donc angles égaux etc
et qui dit cercles avec des angles dit relation angulaire de cocyclicité.
les angles à "chasser" sont encore plus visibles dans le cas où S, P, 1 sont dans cet ordre
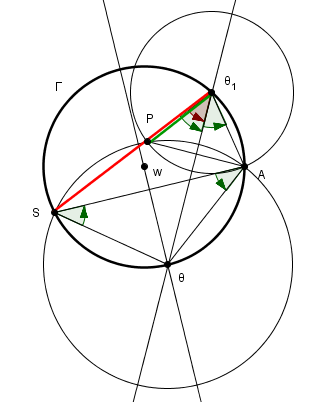
car alors les angles orientés sont équivalents à des angles ordinaires égaux
la principale difficulté dans cette figure est de bien considérer P1 et S1 comme des droites à priori distinctes (en rouge et en vert) pour ne pas se laisser illusionner par des propriétés non démontrées. et faire ainsi une fausse démonstration.
forcer son cerveau à ne pas croire ses yeux, en quelque sorte
on peut aussi faire une figure volontairement fausse
cela dit comment expliquer le fonctionnement de sa pensée est une exercice difficile ...
Annuler
connectez vous