Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première LimitesTopics traitant de limites [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Les limites , une limite qui m'a distrait

Posté par
DR-Youness 28-02-12 à 18:37

Salut à tous ,

Vous pouvez d'abord m'aider à trouver la limite de cette fonction (en attachement) si vous ne voyer pas la photo c'est son lien : http://img20.imageshack.us/img20/8053/codecogseqn1.gif :


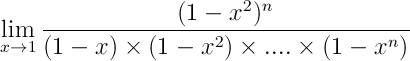
Les limites , une limite qui m\'a distrait

j'ai essayé d'utiliser mais j'ai pas une bonne idée si vous avec des méthodes vous pouvez me sauver , merci

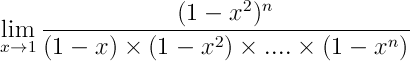
Les limites , une limite qui m\'a distrait

Posté par
pgeodre : Les limites , une limite qui m'a distrait 28-02-12 à 18:58


(1 - x²)n = (1 + x)n (1 - x)n

montre qu'au dénominateur on peut mettre (1 - x)n en facteur
et donc simplifier l'expression par (1 - x)n

Posté par
Glapion Moderateurre : Les limites , une limite qui m'a distrait 28-02-12 à 19:02

Bonsoir, tu peux l'écrire \dfrac{(1-x^2)}{1-x}.\dfrac{(1-x^2)}{1-x^2}.\dfrac{(1-x^2)}{1-x^3}...\dfrac{(1-x^2)}{1-x^p}...\dfrac{(1-x^2)}{1-x^n}

le premier terme tend vaut 1+x et tend vers 2, le second vaut 1, mettons les de coté car ils sont spéciaux et regardons les autres. Vers quoi tend un terme comme \dfrac{(1-x^2)}{1-x^p} ? il s'écrit \dfrac{(1-x)(1+x)}{1-x^p}

On sait vers quoi tend ,\dfrac{1-x^p}{1-x}=1+x+...+x^{p-1}, ça tend vers p-1
Et donc le terme \dfrac{(1-x^2)}{1-x^p} tend vers 2/(p-1) et donc le produit tend vers 2\prod_{p=3}^n\dfrac{2}{p-1}=\dfrac{2^{n-2}}{2.3....(n-1)}=\dfrac{2^{n-2}}{(n-1)!}

Posté par
DR-Younessre : Les limites , une limite qui m'a distrait 28-02-12 à 19:17

Merci monsieur Glapion mais nous avons pas étudier le factoriel pour le moment ^^ mais merci pour ton aide l'idée est arrivée <3

Posté par
Glapion Moderateurre : Les limites , une limite qui m'a distrait 28-02-12 à 19:24

C'est pas grave, laisse là sous la forme juste avant. Tu vois que c'est le produit de termes tous inférieurs à 1 donc ça ne dépasse jamais 1

Posté par
DR-Younessre : Les limites , une limite qui m'a distrait 28-02-12 à 19:29

Merci beaucoup Monsieur Glapion


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1715 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !