Inscription / Connexion Nouveau Sujet
Les suites
 Devoirs33
Devoirs33Bonjour à tous
Pouvez-vous m'aider pour cet exercice. Merci.
a) (un) est une suite arithmétique de raison r.
u2 = 14
u6 = 46
Calculer la raison de cette suite.
Calculer le premier terme de cette suite.
J'ai fait :
Un = Um + ( n - m ) r
U6 = U2 + ( 6 - 2 ) r
46 = 14 + 4r
46 - 14 = 4r
32 = 4r
r = 32 / 4 = 8
Un = U0 + n r
U2 = U0 + 2 * 8
14 = U0 + 16
U0 = -14 + 16
U0 = 2
b) Ecrire un uniquement en fonction de n.
(Un) : { u1 = 8 un+1 = 9 + un
c) Soit (un) une suite arithmétique de raison -1/10 et dont le premier terme est u0 = 6
Calculer u0 + u1 + u 2 ... + u10
On donnera un résultat approché au centième.
Merci.
Je me suis trompée d'énoncé pour les 3 exercices. Désolée, je recommence donc tout.
a) un) est une suite arithmétique de raison r.
Calculer la raison de cette suite :
u4 = -17
u7 = -23
J'ai fait :
Un = Um + ( n - m ) r
U7 = U4 + ( 7 - 4 ) r
U7 = U4 + 3r
-23 = - 17 + 3r
-23 + 17 = 3r
-6 = 3r
r = -6 / 3 = -2 ?
Calculer le premier terme de cette suite
Un = U0 + n r
U7 = U0 + 7 * (-2)
-23 = U0 - 14
U0 = -14 + 23
U0 = 9 ?
b) Ecrire un seulement en fonction de n
(un) : { u0 = 7 / un+1 = -9 + un
c ) Soit (un) une suite arithmétique de raison 3 / 10 et dont le premier terme est u0 = 6
Calculer u0 + u1 + u 2 ... + u7
On donnera un résultat approché au centième.
On me donne u0 = 6
un = u0 + n r
u1 = u0 + n r
u1 = 6 + 1 * 3/10 = 6,3
u2 = 6,3 + 2 * 3/10 = 6,9
a) oui
non. Vous ajoutez quel nombre aux deux membres de l'égalité pour obtenir
c attention revoir la table de 3
b) Ecrire un seulement en fonction de n
(un) : { u0 = 7 / un+1 = -9 + un
Je sais que :
Un+1 = -9 + Un est une suite arithmétique de type Un+1 = Un + r
U0 = 7
de raison r = -9
J'utilise : Un = Um + ( n - m) r
Un = Um + ( n - m ) -9
On vous dit
Vous voulez utiliser
L'indice que l'on a, est 0 ce qui veut bien dire que pour obtenir cela, il faut bien prendre comme indice au lieu de 0
Dans d'autres cours on donne
Remarque : écrit comme cela on a tendance à lire une soustraction que la multiplication par
Il vaudrait mieux soit mettre des parenthèses soit placer ce nombre devant
Oui j'ai aussi cette formule qui représente l'expression de la suite arithmétique
Un = Um + (n - m) r
Un = U0 + (n - m) r
Un = 7 + ( n - 0 ) - 9 ?
Mais nous n'avons pas n
Normal que l'on ne connaisse pas puisque l'on demande de l'écrire en fonction de
on peut l'écrire aussi tout simplement
c ) Soit (un) une suite arithmétique de raison 3 / 10 et dont le premier terme est u0 = 6
Calculer u0 + u1 + u 2 ... + u7
On donnera un résultat approché au centième.
On me donne u0 = 6
un = u0 + n r
u1 = u0 + n r
u1 = 6 + 1 * 3/10 = 6,3
u2 = 6,3 + 2 * 3/10 = 6,9
u3 = 7,8
u4 = 9
u5 = 10,5
u6 = 12,3
u7 = 14,4 ?
On a mais certainement pas
il ne faut pas mélanger la définition explicite et la définition par récurrence
Connaissez-vous la somme des termes d'une suite arithmétique ?
Oui : S =( nombre de termes à additionner / 2) * ( 1er terme + dernier terme)
Je trouve :
u1=6,3
u2=6,6
u3=6,9
u4=7,2
u5=7,5
u6=7,8
u7=8,1 ?
C'est déjà beaucoup mieux
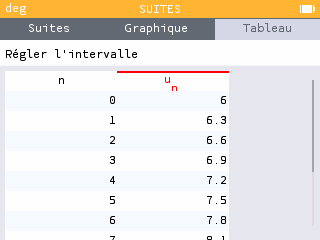
Pourquoi calculez-vous tous ces termes alors qu'il suffit d'appliquer la relation.
Heureusement que l'on ne demandait pas jusqu'à 100 !

S =( nombre de termes à additionner / 2) * ( 1er terme + dernier terme)
s =( 7 / 2 ) * ( 1 + 7 ) = 10,5 ?
On ne prend pas les indices, mais les éléments de la suite
Quels sont les éléments de la suite ?
On ne laisse jamais 8/2
Je n'ai pas compris
J'ai suivi l'exemple de mon cours qui est le suivant :
S est la somme des 1er termes d'une suite arithmétique de 1er terme et de raison 2
Donc on a : S = 50 / 2( 1 + 99 ) = 25 * 100 = 2 500
En revanche, je n'ai pas compris le terme à additionner
Les éléments de la suite ont ceux que vous avez calculés 14 : 34
Il est tellement plus simple d'écrire 4 au lieu de
Dans l'exemple que vous citez, vous avez et
le cinquantième terme est , c'est-à-dire
nombre de termes de 0 à 49 inclus 50
premier terme dernier terme
donc dans l'exercice :
premier terme u0 = 6
dernier terme u7 = 8,1 ( nous l'avons calculé )
S7 = 8 * ( 6 + 8,1 ) / 2
= 4 * ( 6 + 8,1) = 56,4 ?
c) Pour le résultat approché au centième : nous trouvons 56,4.
Je dois donner une valeur approchée au centième donc c'est 56,40 ?


