Inscription / Connexion Nouveau Sujet
lieu géométrique d'un point
Bonjour à tous,
Je suis tombé sur le problème suivant.
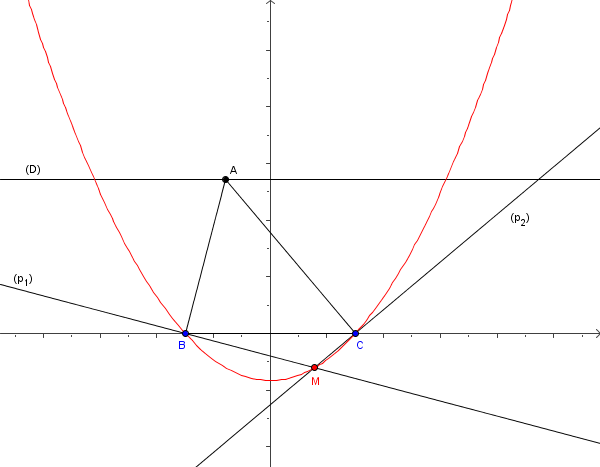
Soit un triangle quelconque ABC, D la droite parallèle à (BC), et M le point d'intersection des perpendiculaires p1 (passant par B et perpendiculaire à (AB) ) et p2 (passant par C et perpendiculaire à (AC) ).
Il faut trouver le lieu décrit par M si A parcourt D.
J'ai commencé par introduire une repère orthonormé avec O=mil[BC].
et puis on constate que si A a comme coordonnées (0,1) alors ABCM est un losange. Et dans ce cas M(0,-1) est le sommet d'une parabole.
Mais comment peur on démontrer analytiquement ce résultat?
Merci pour toute aide
Marc
Bonjour,
Je suppose que (D) est la parallèle à (BC) passant par A;
Le repère choisi est bon.
Dans ce repère, les coordonnées des points sont:
B(-a,0) C(a,0) A(u,b) où u est paramètre (A est un point de D d' équation y=b) et a,b sont fixés.
Equation de (:
on a pour l' équation de :
on a pour l' équation de :
(de la même manière)
M intersection de et
a pour coordonnées (à toi de faire les calculs):
M appartient donc à la parabole d' équation:
Merci beaucoup
Le problème pour moi était que je ne savais pas par oû commencer, apres avoir introduit le repère, afin de parvenir au systeme pour trouver les coordonnées de M.
Mais maintenant c'est tout clair
Merci encore un fois!


