Inscription / Connexion Nouveau Sujet
limite avec paramètre
salut,
soit la fonction f et m un paramètre réel
1) pour m=-2 calculer la lim de f en +∞ et la lim de (f(x)+5x) en -∞ et étudier la limde f en 1
2) pour m=1 étudier la lim de f en 1 et la lim de [f(x)-f(1)]/(x-1)
3) discuter suivant m , lim de f en 1 et la lim de f en +∞

bon pour 1) m= -2 , f(x)= (3x^3-2x²+2x-3) /(x-1) si x>1 et f(x)=[racine de (9x²+2x+5)]-2x-1 si x=< 1
donc lim de f en +∞ =lim de 3x^3/x= +∞
la limite de f en 1 , j'ai utiliser la 2ème expression de f (pour x=<1) et j'ai trouver 1 !!
voilà ce que j'ai compris pour cet exercice !
aidez moi s'il vous plais et merci d'avance
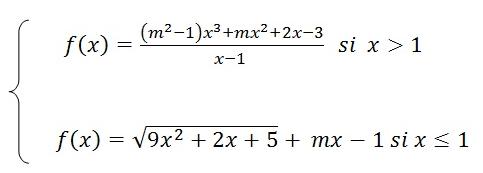
ok 
pour 2) pour m=1 , j'ai trouver la lim de f en 1 =4 ( j'ai utiliser la 2ème expression),
pour la lim de [f(x)-f(1)]/(x-1)en 1 j'ai utiliser aussi la 2ème expression de f et j'ai trouver 21/8
ça reste pour la dernière question ;
* pour la limite de f en 1 j'ai utiliser la 2ème expression de f et j'ai trouver m+3 mais je ne sais pas comment discuter cette limite suivant m 


* pour la lim de f en +l'infinie, je l'étudie pour m=1 et m différent de 1 et pour le 2ème cas , il l'y a 2 cas ; pour m<1 et m>1
c'est ça !!?
, ok pour le 2.
3)m+3 est juste, mais la discussion, s'il discussion il y a, serait bien pauvre. ...
Pas pour . Pour m=1, forme indéterminée
. Utilise la règle de l'Hospital 2 ou 3 fois pour ce cas.
Le signe de influe sur celui de l'infini vers lequel tend f(x).
mais pour m=1 , f(x)=(x²+2x-3)/(x-1) donc la lim de f en +infinie= limite de x²/x= +infinie
et pour m différent de 1, limite de f en +infinie=limite de (m²-1)x^3/x =lim de (m²-1)x² donc cette limite dépend du signe de m²-1


