Inscription / Connexion Nouveau Sujet
Limite d’une Suite
Bonjour, j'ai un exercice à faire avec en seule aide une leçon dans le livre qui ne m'aide pas beaucoup 😅
Voici l'exercice :
Le glacier d'Aletsch, situé dans le sud de la Suisse est le plus grand glacier des Alpes. En 2010, sa longueur était de 22,7 km.
A cause du réchauffement climatique, la longueur de ce glacier diminue de 2 pour-cent tous les 10 ans depuis 2010. On modélise par une suite (Un) la longueur, en kilomètre, du glacier d'Aletsch après n dizaines d'années.
1) Exprimer Un+1, en fonction de Un, puis Un en fonction de n
2) Tabuler la suite (Un) a l'aide de la calculatrice
3) Conjecturer la limite de la suite (Un). Interpréter le résultat pour cette situation
Pour la 1e question j'ai écrit : Pour tout entier naturel, n Un+1= (1-2/100)Un=0.98Un
Ensuite je ne connais pas le mot « tabuler » même en cherchant sur internet je ne comprends pas du tout ce qu'il faut faire
Merci pour tout aide qui me sera apportée !
Bonjour
d'accord
donc est une suite
voir cours et ensuite terme général
On vous demande les termes successifs de la suite soit avec un pas de 1 ou un pas d'une autre valeur à fixer afin de répondre à la question 3
Oui, il faudrait préciser le premier terme et la raison
Vous avez ensuite dans le même cours en fonction de
Problème pour la calculatrice ? Si oui quel modèle ?
( Un) est une suite géométrique de raison 0,98. Ainsi pour tout entier naturel ´, Un=22,7x 0,98n ( exposant)
fonction en surbrillance ok
s'affiche ajouter une fonction ok
f(x)= vous complétez sur la ligne de saisie par 22.7 0.98 x^y x exe
x^y est une touche de la calculatrice
Vous remontez sur fonction puis allez sur tableau exe
Je suis obligée d'aller dans fonction? Je ne peux juste pas aller dans les suites ?
Pour la question 2 j'ai fait un tableau avec pour Intervalle de n 10
Et pour la question 3 j'ai écrit il semble que Un est aussi proche de 1 que l'on veut lorsque n est suffisamment grand.
1<Un< 18,5 pour tout entier naturel >10
1<Un< 6,7 pour tout entier naturel >60
On dit que la suite (Un) a pour limite 1 et on note
Lim ( n->+ infini) Un=1
Si cela revient au même
Pourquoi 1 ? Une suite géométrique de raison comprise entre 0 et 1 tend vers 0 quand tend vers
À terme le glacier disparaîtra
Donc à chaque fois que la limite est en dessous de 1 je peux simplement écrire 0 , en tout cas je vous remercie ! J'étais perdue , merci beaucoup
En prenant un tableur avec un pas de 10 on a
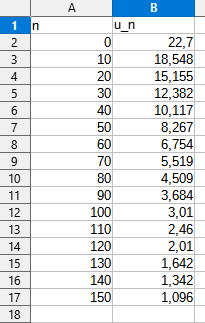
ce qui montre que dans 15 siècles il restera un glacier de 1,096 km
On ne peut pas dire qu'en dessous de 1 c'est 0
De rien


