Inscription / Connexion Nouveau Sujet
Loi Binomiale
Bonjour,
Je m'appelle Emilie et je suis actuellement en classe de terminale option mathématiques .J'ai un DM à rendre pour mardi et je bloque sur certaines questions.
J'ai commencé à résoudre le problème ci-dessous mais serait-il possible de me dire si ce que j'ai fait est juste et comment terminer le problème ?
Merci d'avance aux personnes qui prendront le temps de m'aider.
Bonne journée
La compagnie « in the air » dispose d'un avion de 240 places pour un vol intérieur. On considère que les comportements des passagers sont indépendants les uns des autres et on évalue à 0,9 la probabilité qu'un passager soit présent à l'embarquement. On suppose dans cette partie que la compagnie a vendu exactement 240 places et on nomme X la valeur aléatoire égale au nombre de passagers embarquant parmi les 240 possibles.
1) Justifier que X suis la loi binomiale de paramètres n= 240 et p=0,9
2) Quelle est l'espérance de X ? Interpréter ce nombre dans le contexte.
3) Calculer
. Donner une interprétation de ce nombre expliquant la nécessité pour la compagnie d'avoir recours à la surréservation.
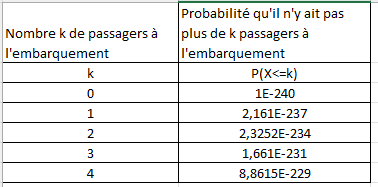
4) À l'aide d'un tableur, reproduire la feuille de calcul ci-contre. Déterminer alors le plus petit entier k tel que , puis interpréter le résultat.
(voir image)
Voici le début de mes réponses.
1) La solution correspond à un schéma de Bernoulli d'ordre 240 car c'est la répétition de 240 épreuves de Bernoulli identique et indépendante où :
S = le passager est présent à l'embarquement
p(S) = la probabilité qu'un passager soit présent à l'embarquement = 0,9
Comme X compte le nombre de succès, X suit alors la loi binomiale de paramètres n=240 et p=0,9
2) Si X suit la loi Binomiale de paramètres n=240 et p=0,9 alors on admet E(X)= n*p= 240 * 0,9 = 216
La compagnie considère donc que sur 240 passagers, en moyenne 216 seront présents à l'embarquement.
3) = 1 - p(X=220)
p(X=k) =
p(X=220) = = 0,06
= 1 - p(X=220) = 1-0,06= 0,94
La probabilité qu'il y ait 219 passagers ou moins est p=0,94.
Sachant qu'il y a 240 places dans l'avion, la surréservation est donc nécessaire.
salut
2) Si X suit la loi Binomiale de paramètres n=240 et p=0,9 alors on admet donc E(X)= n*p= 240 * 0,9 = 216
La compagnie considère donc que sur 240 passagers, en moyenne 216 seront présents à l'embarquement.
3/ non ça ne va pas !!
P(X <= 219) = P(X = 0) + P(X = 1) + ... + P(X = 218) + P(X = 219)
mais tu calcules directement P(X <= 219) avec la calculatrice
Bonjour et merci pour votre retour,
si je change le verbe considère par estime , est-ce mieux ?
Pour la question 3, je ne comprends pas votre retour.
Si j'utilise la formule ou je calcule directement P(X<=219) avec ma calculette (je ne sais pas faire), je dois trouver le même résultat, non ?
Merci d'avance
ce n'est pas la compagnie qui considère ou estime ...
c'est plutôt un constat ... de la théorie ... mais c'est un "détail"
non ce que tu as écris est faux : le contraie de l'événement X =220 est
(X= 0) U (X = ) U ... U (X = 218) U (X = 219) U (X = 221) U ... U (X = 240)
tout sauf 220
mais tu veux X <= 219
et à ton niveau il n'y a qu'avec la calculatrice ...
donc il faut apprendre à s'en servir et tu trouveras comment sur internet en tapant la bonne requête ...
Alors je pense avoir trouvé le bon programme sur ma calculatrice  .
.
binomFRep(240,0.9,219) = 0.77
Ce qui signifierait que la probabilité qu'il y ait 219 passagers ou moins est de 0,77 d'où la nécessité de surréservation.
très bien ... en faisant attention aux valeurs approchées :
binomFRep(240,0.9,219)
 0.77
0.77
Ce qui signifie rait que la probabilité qu'il y ait 219 passagers ou moins est de environ 0,77 d'où la nécessité de surréservation.

et pour la rédaction sur ta copie écris simplement :
d'après la calculatrice P(X
 219)
219)  0,77
0,77
(le correcteur n'ayant pas nécessairement la même calculatrice que toi, tu lui indiques "mathématiquement" ce que tu calcules ... même si dans le cas présent c'est écrit explicitement dans la question ... mais ça aurait pu être demandé en français)

Bonjour et merci pour la confirmation.
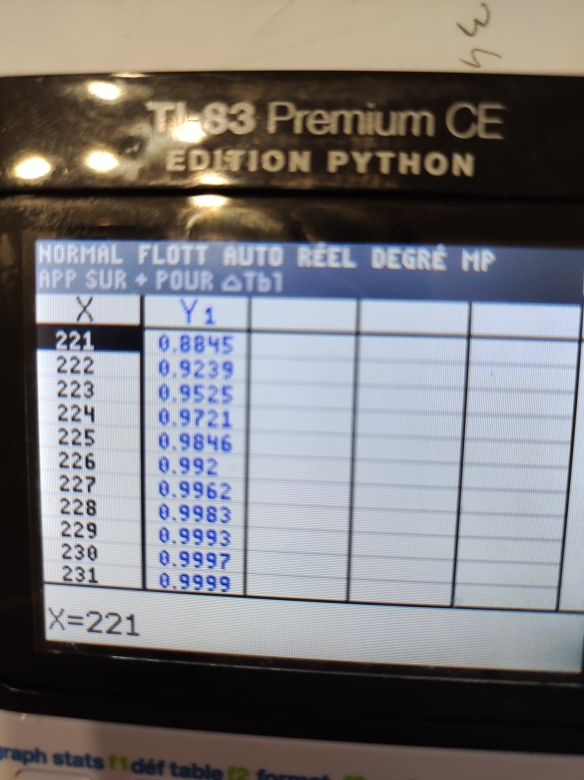
pour la question 4, il nous a été indiquer par notre professeur d'utiliser la table de la calculatrice.
J'ai finalement trouvé comment créer la table mais je ne suis pas certaine de mon interprétation.
p(X<=k)>=0,95
Selon mon tableau, je dirai que k=223
Est-ce correct ?
Merci d'avance
Merci beaucoup, je dois maintenant m'attaquer à la partie B !
Partie B : Etude du risque de surréservation
1) Quel est le taux de surréservation, c'est à dire le rapport entre le nombre de places vendues au-delà de la capacité de l'appareil et cette même capacité ? On exprimera le résultat en pourcentage, arrondi à 0,1%
2) On note Y la variable aléatoire égale au nombre de passagers se présentant effectivement à l'embarquement. Déterminer la loi suivie par la variable aléatoire Y et en préciser les paramètres.
3) a) pour quelle valeur de Y la compagnie devra-t-elle refuser des passagers à l'embarquement ?
b) Déterminer la probabilité que la compagnie doive refuser au moins un client.
4) La compagnie souhaite connaître le nombre maximal de places à mettre en vente pour que le risque qu'elle doive refuser au moins un client soit inférieur à 1%.
Autrement dit, elle cherche le plus grand entier n tel que p(Z>240)<=0,01 lorsque Z suit la loi binomiale de paramètres n et p=0,9 avec n>= 240.
A l'aide de la table de la calculatrice, déterminer cette valeur de n.
Quel est alors le taux de surréservation ?
1) taux de surréservation = nombre de places vendues au delà la capacité de l'appareil / capacité de l'appareil
donc Taux de surréservation= 17/240= 0,0708 soit 7.1%
2) Y suit une loi binomiale de paramètres n=257 et p=0,9
Correct ?
Oups désolée effectivement, la phrase manquante est :
La compagnie a vendu 257 places alors qu'elle n'en dispose que de 240.
Je n'ai pas encore terminé l'exercice ci-dessus mais j'ai bien avancé le deuxième exercice de probabilités. J'ai répondu aux question mais je suis bloquée à partir de la 4c. Pourriez vous me confirmer que mes réponses sont correctes et m'indiquer comment poursuivre ?
D'avance merci à tous.
Bonne soirée
Exercice 2 :
Un joueur tire au hasard des cartes dans un jeu de 32 cartes jusqu'à obtenir un as.
Soit X la variable aléatoire comptant le nombre de cartes tirées par le joueur.
1) Justifier que X suit une loi géométrique dont on précisera le paramètre.
2) Calculer l'espérance mathématique de X. En donner une interprétation dans le contexte de l'exercice.
On donnera le calcul effectué (simplifié) et une valeur approchée à 0,001 près de chaque probabilité demandée.
3) a) Calculer p(X=8). En donner une interprétation dans le contexte de l'exercice
b) Calculer p(X <=8). En donner une interprétation dans le contexte de l'exercice
c) Calculer p(X>10) sachant (X>4)
4) Calculer la probabilité des évènements suivants :
a) « le joueur a tiré 5 cartes pour obtenir un as »
b) « le joueur a tiré au moins 5 cartes pour obtenir un as »
c) « le joueur a tiré moins de 10 cartes pour obtenir un as »
5) Le joueur a tiré 8 cartes sans obtenir d'as.
Quelle est la probabilité qu'il doive en tirer moins de 13 pour obtenir un as ?
Mes réponses:
1) X suit une loi géométrique car c'est la répétition d'épreuves de Bernoulli (as ou pas as donc gagnant ou perdant), identique et indépendantes où S="la carte tirée est un as"
p(S) = 4/32 = 1/8 = 0.125
Comme X compte le nombre d'épreuves pour obtenir un succès, X suit alors la loi géométrique de paramètres p=0,125.
2) E(x) = 1/p = 1/0.125 soit environ 8
En moyenne, le joueur doit tirer 8 cartes pour obtenir un as
3) a) p(X=k) =
p(X=8) = = 0,049
La probabilité que le joueur tire un as en ayant tiré 8 cartes est de 0,049
b) p(X<=k) =
p(X<=8) = = 0,656
La probabilité que le joueur tire un as en ayant tiré au plus 8 cartes est de 0,656
c)
=
=
= 1 - p(X6)
= 0,449
4) a) p(X=5)= = 0,073
b)
=
= 0,586
attention !!
pour un autre exercice tu dois créer un nouveau fil ...
fais un copier-coller du code de ce que tu as écrit et ouvre un autre sujet
pour obtenir le code de ce que tu as écrit : dans la ligne où se trouve ton pseudo tu vas à droite et clique sur la première icone (une sorte de infini) et sélectionne tout (avec un clic droit)
Merci beaucoup pour l'information 
J'avais essayé mais j'ai cru que cela allez faire un multi-post.
Je viens donc de le reposter sous le nom Tirer un as.
Encore merci pour votre aide.


