Bonjour,

Pas vérifié tes résultats, mais il y a une relation toute simple entre variance et écart-type ...

Bonsoir,
Attention, tes probas sont fausses, tu fais comme si on tirait une seule boule.
Et du coup, tu oublies le cas où on tire 2 jaunes

Bonjour co11

Je vous laisse

Et on tire de nouveau .....
Si tu faisais un arbre par exemple, il n'y a que 2 tirages.

Bonsoir littleguy  

D'accord co11 mais ducoup si on tire deux jaunes on a aussi une probabilité 5/20 ?
Mais dans ces cas là ce n'est pas correct car le totales des probabilité est > 1

Non, fais donc un arbre j'insiste

Voilà mon arbre mais je le pense faux car sinon cela ne nous servais à rien de nous dire que 15 boules sont rouge et 5 sont jaune...

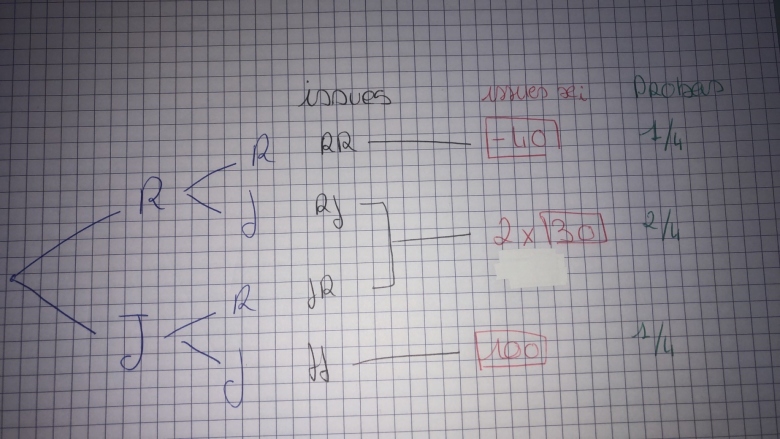
Attention,
sur chaque branche menant à R, la proba est 15/20 soit 3/4, et sur chaque branche  menant à J c'est 1/4.
Donc, par exemple P(R, R) = (3/4)²
Tu poursuis ?

Et je reviens à ton post de 18h41, tu fais comme si les 4 issues avaient la même proba mais ce n'est pas le cas : pas le même nombre de boules rouges et jaunes

Bah dans ce cas là :

P(R, R) = (3/4)² =0,5635
P(R, J) = 2*[ (3/4) + (1/4) ] = 2
P(J, J) = (1/4)² = 0,0625

C'est pas possible, si?

D'accord donc

P(R, R) = (3/4)² = 0,5635
P(R, J) =  (3/4) * (1/4) = 3/16 = 0,1875
P( J, R) =  (1/4)*(3/4) = 3/16 = 0,1875
P(J, J) = (1/4)² = 0,0625

Soit 0,5635 + 0,1875 + 0,1875 + 0,0625 = 1,001 = 1

Donc

Ok.

Donc ducoup :

2) E(X) = -5,03                  σ(X) = 42,86

V(X) = Utilise t-on la formule :

3) Sur un grand nombre de répétition on perd en moyenne 5,03  €

4) Non, car -5,03   0

Pause repas, à plus

J'ai l'impression que la  question 2) demande une utilisation de la calculatrice : des listes ?
Cela dit, E(X) = 5 exactement
Oui pour ... quoique j'ai tendance à arrondir donc plutôt 42, 87
Pour la variance, oui (X)  =
Mais si la calculatrice est attendue, il faut lire la ligne :

Pardon E(X) = - 5 et non 5

D'accord mais avec la calculatrice il nous faut des donnée supplémentaire ou alors on utilise la formule
V(X)= p₁(x₁ -E(X))² + p₂(x₂ -E(X))² + p₃(x₃ -E(X))² + ...

Pour moi, à calculatrice, il faut entrer les valeurs en liste 1 (L1), les probas en liste 2 (L2)et demander à la calculatrice de faire les calculs.
Bon, moi j'ai une TI, et toi ?
Mais pour ce soir j'arrête, à demain ?

Casio et je ne sais pas comment faire,
Je vais donc pas défaut utilisé la longue formule, je vous souhaite donc une bonne soirée co11

Bien évidement je n'attend pas votre réponse ce soir, j'ai trouvé V(X) = 1838,7

Bonjour, est-ce que ma réponse V(X) = 1838,7 est correcte?

Bon, je n'ai plus de casio, donc je vais avoir du mal (impossible de vérifier)
Ta valeur 1838, 7 n'est pas loin en tout cas.
Et à part ça, avec 42, 87, on o btient : V(X) 1837, 84

Très bien, je vous remercie co11, je vous souhaite une bonne soirée.🤗

Et sinon, la longue formule me donne:
V(X) = (1600*9 + 900* 6 + 10000) /16 - 5² = 1837,5

J'essaie de t'expliquer un peu ce qu'il faudrait faire avec ta calculatrice :
Dans le menu tu choisis "STAT"
Normalement des listes doivent apparaître (nommées List 1, List2 .....)
Tu rentre les valeurs de la variable aléatoire en List1
                      les probas en List 2
Ensuite tu peux demander à la calculatrice d'afficher certains résultats : moyenne (espérance) notée , .....
Pour cela, dans "STAT", il faut sélectionner "CALC" puis "SET" pour expliquer à la calculatrice comment lire les données :

Bon, c'est un peu rapide mais il doit y avoir des détails dans ton livre.
Et sinon, tu peux voir un site qui s'appelle : "36 élèves 36 calculatrices" que je trouve très pédagogique, mais peut-être pas mis à jour ...?

Si tu y arrives, un des résultats affichés devrait être : x² = 1862,5
Il s'agit de la somme des p_ix_i²
C'est presque la variance (deuxième formule)