Bonjour,

J'ai un exercice que je n'ai pas du tout compris et dont j'ai la correction mais que je ne comprends pas non plus. Je n'arrive même pas à démarrer donc je n'ai rien fait...

Pouvez-vous me venir en aide s'il vous plait ? :/

Voilà le sujet :

Le Paradoxe de Bertrand

Soit un cercle C de rayon 1, le côté d'un triangle équilatéral inscrit dans ce cercle est alors égal à .

Le but de cet exercice est d'étudier différentes méthodes pour déterminer la probabilité qu'une corde du cercle, choisie au hasard, ait une longueur supérieure à .


_{* Tom_Pascal > image placée sur le serveur de l', merci d'en faire autant la prochaine fois Justme-974 *}

1- Première méthode

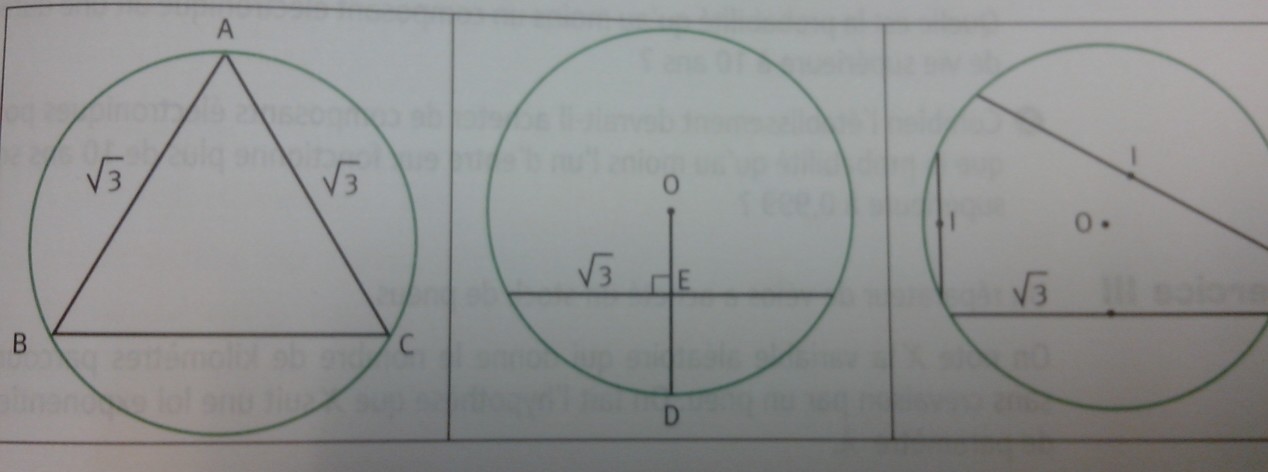
On fixe un point A sur le cercle C. On choisit au hasard un point M sur le cercle et on considère la corde AM. Quelle est la probabilité que la corde AM ait une longueur supérieur à ? ( On pourra utiliser les point B et C du cercle tels que le triangle ABC soit équilatéral.)

2- Deuxième méthode

Soit O le centre du cercle et D un point du cercle. On choisit au hasard un point I sur le segement [OD]. Quelle est la probabilité que la corde de milieu I ait une longueur supérieure à ?

3- Troisième méthode

On choisit au hasard un point I à l'intérieur du cercle. Quelle est la probabilité que la corde de milieu I ait une longueur supérieur à ?

4- Commenter les résultats précédents.

Je vous remercie d'avance pour votre aide car je n'ai vraiment rien fait :/