Inscription / Connexion Nouveau Sujet
Maximum de points frontaliers
Bonjour à tous 😊
Une petite question que je me suis posée et à laquelle je n'ai pas de réponse :
On dessine un triangle dont les sommets sont aux nœuds d'un quadrillage orthonormé et qui contient un unique nœud du quadrillage en son intérieur . Existe-t-il un nombre maximal de nœuds à sa frontière ? J'ai plusieurs exemples avec 8 nœuds mais pas au-delà .
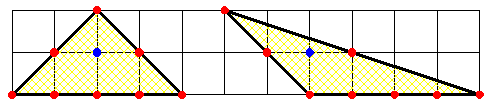
Merci d'avance pour la participation 😊
Imod
Bonjour,
Je pense avoir trouvé un triangle avec 9 nœuds.
Je ne suis pas chez moi ; je donne donc ma réponse sans figure, avec les coordonnées des sommets :
 Cliquez pour afficher
Cliquez pour afficherOui , bien vu Sylvieg 
Une remarque , avec la formule de Pick , il suffirait de trouver un maximum pour l'aire du triangle . J'étais à 4 et tu viens de franchir 4,5 
Imod
En fait, il y en a plein avec 9 nœuds, dont un très simple :
 Cliquez pour afficher
Cliquez pour afficherCe n'est pas surprenant , si le nombre de nœuds à la frontière et à l'intérieur est donné , l'aire est fixée .
Ce qui semble plus étrange c'est qu'avec aucun nœud à l'intérieur on peut faire grandir l'aire comme on veut mais pas avec un seul nœud .
Imod
J'ai fini pas trouver une réponse complète au problème avec un ou même plusieurs nœuds à l'intérieur du triangle . Comme le plaisir est dans la recherche ( pas uniquement sur le net ) , je vous laisse cogiter et ( j'espère ) apprécier 
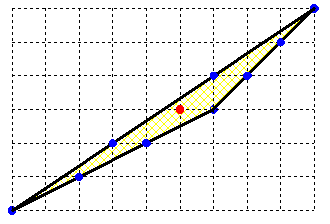
Imod
Bonjour Imod,
En déplacement en ce moment, je suis moins disponible.
Je reprendrai le fil à mon retour à la pentecôte.
C'est un sujet intéressant.
En particulier, ce que remarque lmod :
Ce qui semble plus étrange c'est qu'avec aucun nœud à l'intérieur on peut faire grandir l'aire comme on veut mais pas avec un seul nœud .
Je suis content de voir que certains ne lâchent pas le morceau 
Vous m'excuserez ( j'espère ) de ne pas donner d'indice 
Imod
Bon je n'ai pas une réponse complète mais j'espère apporter de l'eau au moulin:
Par Pick, on a A = i + b/2 - 1, avec A l'aire, i le nombre points à l'intérieur et b le nombre de points sur le bord.
Soit (-u,-v), (0,0) et (x,y) les sommets de notre triangle. Avec u,v,x et y > 0 et v/u < y/x. Le triangle est obtu à l'origine.
On a A = (u+x)(v+y)/2 - uv/2 - xy/2 - vx = (uy-vx)/2
On a b = gcd(u,v) + gcd(x,y) + gcd(u+x, v+y).
Comme on a un point à l'intérieur, celà donne uy-vx = gcd(u,v) + gcd(x,y) + gcd(u+x, v+y).
Si l'on suppose v = v'u et y=y'x de façon à maximiser le nombre de points sur les petits côtés, celà donne:
ux(y'-v') = u+x + gcd(u+x, uv'+xy') <= 2(u+x).
On a donc 0 < y'-v' <= 2(u+x)/(ux).
y'-v' étant entier, ça limite pas mal les possibilités pour (u,x).
Sinon j'ai testé tous les (u,v,x,y) < 100 sans solutions avec une aire > 9 
Bonjour LittleFox
Une idée pour limiter le nombre de cas ( on peut sans doute faire autrement ) , une solution peut se réduire à une autre plus petite dans un sens qu'il faut trouver .
Imod
Bonjour,
Pas de nouvelle car je ne trouve rien d'intéressant 
J'attends patiemment la fin du mois 
En espérant que la ou les solutions ne seront pas au dessus de mon niveau.
Une question en attendant : Pourquoi le triangle aurait-il un angle obtus ?
Bonjour
1°) Il n'y a aucune raison qu'un des angles du triangle soit obtus .
2°) Comme je le signalais à LittleFox , il y a une astuce ( pas facile à trouver ) qui permet de réduire des solutions très étalées à d'autres plus ramassées . Il suffit ensuite d'étudier un petit lot de configurations .
3°) On peut facilement généraliser l'exercice à 2 , 3 , ... points à l'intérieur du triangle , c'est même plus simple car avec 1 point à l'intérieur on a affaire à une sorte d'exception .
Imod
Merci pour ta réponse rapide.
J'ai parlé d'angle obtus suite au message de LittleFox où il démarre ainsi :
Soit (-u,-v), (0,0) et (x,y) les sommets de notre triangle. Avec u,v,x et y > 0 et v/u < y/x. Le triangle est obtu à l'origine.
Tu as raison , attendons la réponse de LittleFox 
Je n'ai pas vérifié tous ses calculs car je suis sûr qu'ils n'épuisent pas tous les cas . La recherche sur un autre nombre de points intérieurs peut aider .
Désolé de ne pas donner plus d'indices 
Imod
Maintenant on peut généraliser :
Quel est le nombre de points maximal à la frontière ( ou quel est l'aire maximale ) du triangle contenant exactement "n" nœuds à l'intérieur ?
Imod
Merci Imod,
J'aurais pu penser à aller voir 
Il y a trois solutions proposées.
Seule celle qui utilise un déterminant m'a convaincue.
Quelque chose doit m'échapper pour comprendre les deux autres ou ton indication 
J'ai regardé plus en détail la solution avec les rectangles dont le périmètre se réduit.
Si j'ai bien compris la transformation dont il est question,
voici un exemple où le périmètre ne se réduit pas :
Bon, il y a plus d'un point à l'intérieur de mes triangles...
Mais ne faudrait-il pas compléter le raisonnement pour justifier que s'il y a un seul point à l'intérieur alors le périmètre du rectangle décroit ?
Tu as raison , la troisième figure de l'illustration est fautive . On peut considérer sans problème que le coin inférieur gauche du rectangle est un point du triangle et alors tout se passe bien .
Imod
Ce n'est pas vrai non plus.
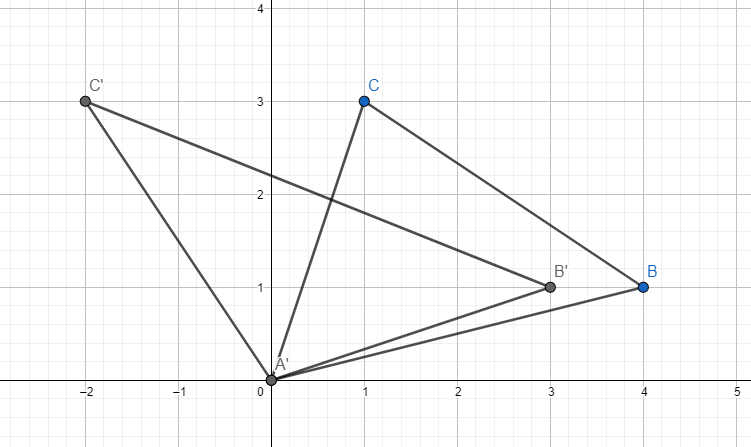
Et il n'y a pas de justification de pourquoi dans les cas de base, a et b prennent leur valeur dans {2,3,4}. Ce n'est pas clair pour un triangle avec une base de 5 qui est aussi un bord du rectangle ne peut pas contenir juste un point.
Comme Sylvieg, la seule démo qui me convainc est celle avec le déterminant. Mais elle n'est pas directement utilisable pour n points intérieurs. Il faut refaire l'analyse de cas.
Étonnant ce site Diophante où des solutions sont publiées sans que, semble-t-il, un minimum de vérification soit faite.
D'ailleurs, je n'ai pas compris comment on pouvait proposer une solution.
Il y a en effet un "bug" dans ma démonstration , je vais voir si je peux la corriger sinon je demanderais à ce qu'on la supprime .
Pour répondre à Sylvieg : Les propositions sont vérifiées par l'auteur du site qui est l'unique vérificateur des solutions . En cas de doute , les autres participants peuvent être mis à contribution ( j'ai personnellement validé la solution de Pierre Renfer ) . La troisième solution est une solution partielle acceptée aussi par le site .
Un doute avait été émis à propos de ma solution .
Pour proposer une solution on "clique" sur le lien et s'il ne fonctionne pas ( c'est souvent le cas ) on en essaie un autre en précisant le problème qu'on vient de résoudre ( on est toujours très bien accueilli ) .
@LittleFox : Pour un côté "5" dans un triangle rectangle , on passe de "0" à deux points quand on augment le deuxième côté .
Imod
Je comprends mieux le fonctionnement du site Diophante .
Dommage que ça n'apparaisse pas dans l'accueil, ou ailleurs.
On peut donc y communiquer par courriel.
Selon moi, la "solution" de Pierre Julien n'est qu'une illustration du problème sans la moindre justification des affirmations qui y figurent. La formule de Pick n'y est même pas évoquée.
Ça rend le site peut crédible...
@LittleFox : Pour un côté "5" dans un triangle rectangle , on passe de "0" à deux points quand on augment le deuxième côté .
Ce genre de justification mériterait d'être écrite dans la démonstration.
Ok dans un triangle rectangle. Quid des autres triangles?
Bonjour LittleFox,
Je pense qu'il faut enlever le mot "triangle" dans la phrase :
Pour un côté "5" dans le rectangle, on passe de "0" à deux points quand on augment le deuxième côté du rectangle.
Tout n'est pas à jeter non plus 
Soit un triangle ABC dont les sommets sont sur les noeuds du quadrillage.
Il peut-être transformé en un triangle dont l'un des côté est parallèle aux axes du quadrillage sans changer son aire ni le nombre de points intérieur.
Les translations, les symétries par rapport aux axes du quadrillage ainsi que (x,y) -> (x,y-x) et (x,y) -> (x-y,x) conservent l'aire et le nombre de points à l'intérieur du triangle.
Par translation on place A à l'origine. Par symétrie on place B = (x,y) dans le premier quadrant (x>=0 et y >=0).
Tant que x > 0 et y > 0, si x < y alors on applique la transformation (x,y) -> (x, y-x) sinon (x,y) ->(x-y,y). A chaque étape B reste dans le premier quadrant mais x+y diminue. Il y a donc une étape où x=0 ou y=0. Lorsque x=0, le segment AB est aligné avec l'axe y et lorsque y=0, le segment AB est aligné avec l'axe x.
Note: cet algorithme est similaire à l'algorithme d'Euclide pour trouver le pgcd.
On peut mettre la base sur l'axe x par la symétrie d'axe x=y.
Il ne reste plus qu'à faire la démonstration pour un triangle dont la base est horizontale.
C'est facilement démontrable pour les triangle dont la base est grande (>3) mais pour les petits, en particulier quand la base = 1, je suis pas sûr de la démarche. En effet, on a facilement des triangles avec 0 ou 2 points alors pourquoi pas 1?
Note: On peut réduire encore une fois le nombre de cas en appliquant les transformation (x,y) ->(x,y x) déplaçant C de sorte que 0 <= x(C) <= y(C).
x) déplaçant C de sorte que 0 <= x(C) <= y(C).
Je laisse au suivant, surtout que ça semble tellement évident à Imod 
Je laisse au suivant, surtout que ça semble tellement évident à Imod

Ne crois surtout pas ça

J'étais persuadé d'avoir "la" bonne idée en réduisant facilement la taille du rectangle tout en conservant les points à la frontière et à l'intérieur . C'était clairement faux . Il est clair qu'à chaque étape on peut changer de repère en inversant les axes , les orientations et l'origine sachant que le but est de trouver quelque chose qui diminue .
Et pourquoi lorsque l'un des côtés du triangle est sur un axe du quadrillage ne peut-on pas poursuivre la stratégie jusqu'à ce qu'il partage complètement un côté du rectangle ?
Désolé pour mon manque de réactivité

imod
On est limité dans la stratégie car une fois AB aligné avec l'axe x, on ne peut plus utiliser (x,y) -> (x,y x) sans bouger B hors de l'axe.
x) sans bouger B hors de l'axe.
En appliquant (x,y) -> (x , y), on peut déplacer C mais seulement horizontalement et par sauts de y(C). Si AB est plus court que y(C) alors dans certains cas on ne pourra pas avoir 0 <= x(C) <= x(B). Cet dernière condition étant nécessaire pour que AB soit un des côtés du rectangle.
, y), on peut déplacer C mais seulement horizontalement et par sauts de y(C). Si AB est plus court que y(C) alors dans certains cas on ne pourra pas avoir 0 <= x(C) <= x(B). Cet dernière condition étant nécessaire pour que AB soit un des côtés du rectangle.
Par exemple le triangle bleu ne peut pas arriver dans le rectangle rouge puisqu'il a 2 points intérieur alors que tous les triangles de base AB et dont le 3ème sommet est dans le rectangle ont 0 points intérieur.
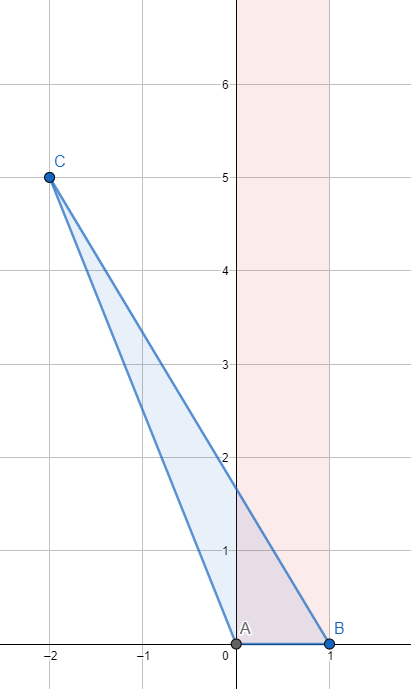
D'accord , on aligne les points A et B sur l'un des axes et on ne peut pas directement les positionner aux sommets du rectangle qui encadre le triangle . On peut tout de même en choisissant par exemple C comme origine amener les points A et B en (0;4) et (1;6) puis continuer les manœuvres . Bien sûr tout ça n'a pas beaucoup de sens si on ne désigne pas précisément la quantité qu'on veut réduire .
Imod
Si on reste sur l'idée de LittleFox , on peut noter que le côté du triangle aligné avec le quadrillage est inférieur ou égal à 4 .
Imod
Oui et on peut aller plus loin:
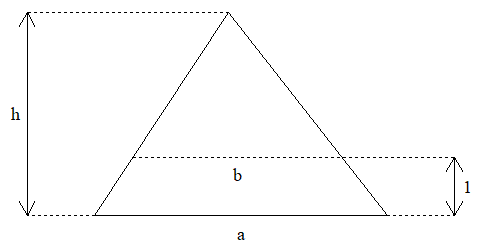
Soit un triangle de base a horizontale et de hauteur h, il contient des segments horizontaux avec y entier pour 0<y <h.
La longueur de ces segments est donnée par
Or ces segments contiennent (en excluant les extrémités) entre et
points du quadrillage.
On a donc que le nombre de points à l'intérieur du triangle est limité par
Ce qui limite les solutions entières avec i = 1.
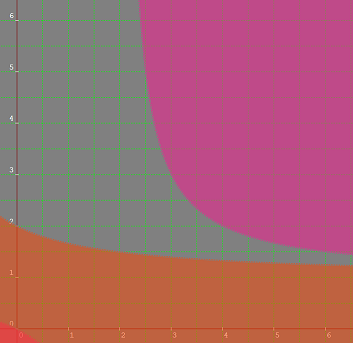
Si en plus on veut ah>9 alors on est limité à a=2 et h  4 ou a=1 et h
4 ou a=1 et h 9.
9.
En fait on peut éliminer facilement les cas a=1 et a=2 :
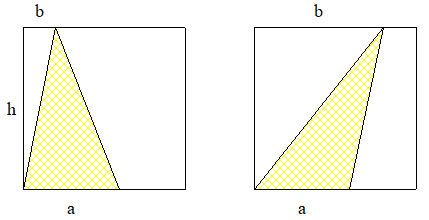
On a et selon le cas ,
ou
. Dans les deux cas la formule de Pick nous dit que le nombre de points à l'intérieur est supérieur à 1 .
Il reste à mettre tout ça au propre 
Imod
Oula, tu vas un peux vite.
Déjà b est déjà pris pour autre chose.
C'est quoi F ?
Je suis d'accord que b<h.
Le triangle (0,0), (0,1), (2,3) a une base de 1 et ne contient qu'un point.

En effet il y a un problème quand a=1 
F est le nombre de points à la frontière du triangle . En fait b est quasiment inférieur à b/2 quand a est petit . J'y retourne 
Imod
Il fau lire "b est quasiment inférieur à h/2 quand a est petit" . Je ne vois rien sur les petits écrans 
Imod
Le cas m'embête toujours un peu mais je pense avoir une généralisation :
ou encore
pour
.
Un seul point intérieur ferait donc exception ?
Imod
Bon en fait le cas a=1 se traite de la même façon que les autres , il y a juste deux cas particuliers .
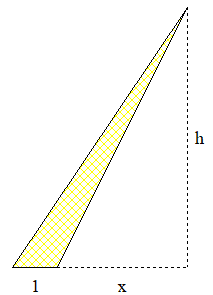
Par transvection on peut supposer que h>2x .
Si h>2x+2 alors I-1=A-F/2 > 0 ce qui est impossible . Sinon h=2x+1 ou 2x+2 et on applique deux nouvelles transvections :
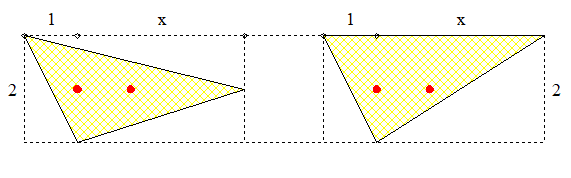
Si h>9 alors x>3 et il y a au moins deux points à l'intérieur .
La démonstration semble tenir debout , on doit pouvoir rendre ça plus homogène , j'y réfléchis ce soir 
Imod
Bon en fait le cheminement est assez simple à résumer ( je rédigerai une solution complète plus tard ) . On suppose par l'absurde qu'il existe un triangle avec une aire supérieure à 4,5 .
Etape 1 : Si aucune paire de points partage la même ligne , on en choisit deux A et B et on les amène sur une même ligne par une succession de transvections . Cette même succession appliquée au triangle ne va pas changer son aire ni le nombre de points intérieurs .
Etape 2 : On réduit la taille du triangle par transvections jusqu'à ce que h>=a+2x ( voir dessins antérieurs ) . On montre alors facilement que a=1 .
Etape 3 : On a a=1 et h>2x .
Si h=2x+1 ou h=2x+2 , on trouve deux points intérieurs en effectuant deux transvections . Sinon on conclut en remarquant que le nombre de points à la frontière est inférieur à h .
Imod
Je propose une solution rédigée au problème avant de regarder le cas de plusieurs points intérieurs .
Imod


malou edit > ** pour plus de lisibilité sur le site **mais bon pour une fois  **
**
C'est très dur à suivre, on saute d'une idée à l'autre, on pose des équations sans explication, on balaie certains cas qui ne sont pas si simples pourtant et il y a des équations fausses.
Dès le début, on suppose par l'absurde puis on pose les transvections alors qu'il n'y a pas de lien.
Ce serait plus clair de découper en lemmes:
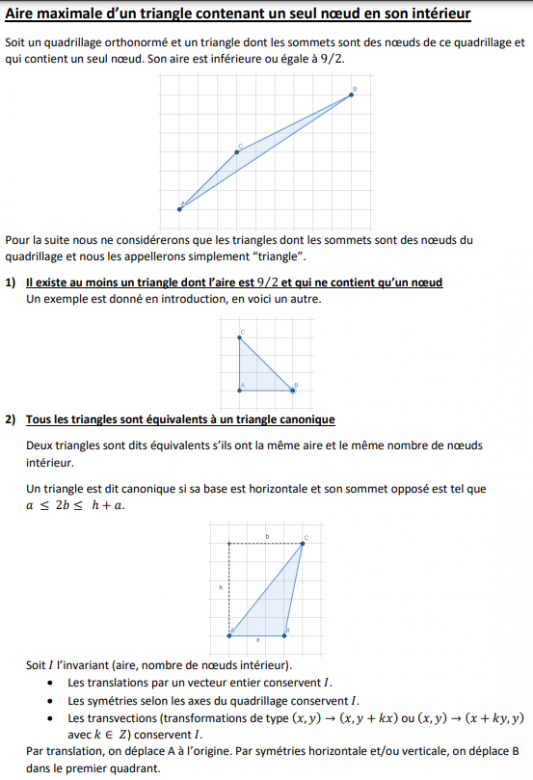
Lemme 1: Pour tout triangle, il y a (au moins) un triangle canonique (base horizontale et sommet (b, h) avec 0 <= 2b <= h+a) qui a la même aire et le même nombre de point intérieur.
Utilisation des transvections (nouveau mot que je ne connaissais pas en français  ).
).
Lemme 2: Il n'existe pas de triangle canonique avec 0 <= b <= a , un seul point intérieur et une aire plus grande que 9/2.
Celui-ci à été balayé par un "Il est clair que l'abaissé du point C sur (AB) se situe au delà du segment [AB] . ". Je ne trouve pas ça clair du tout. Par exemple (0;0), (3;0), (1;5) est en forme canonique mais a son sommet entre A et B.
Lemme 3: Tout triangle canonique avec 2a < 2b <= h+a et au plus un point intérieur a une base de longueur 1 (a = 1).
On peut simplifier la démo: 2b <= h+a, b <= h-x < h et a < y. Puisque (0,0), (a,y) et (b,h) sont alignés.
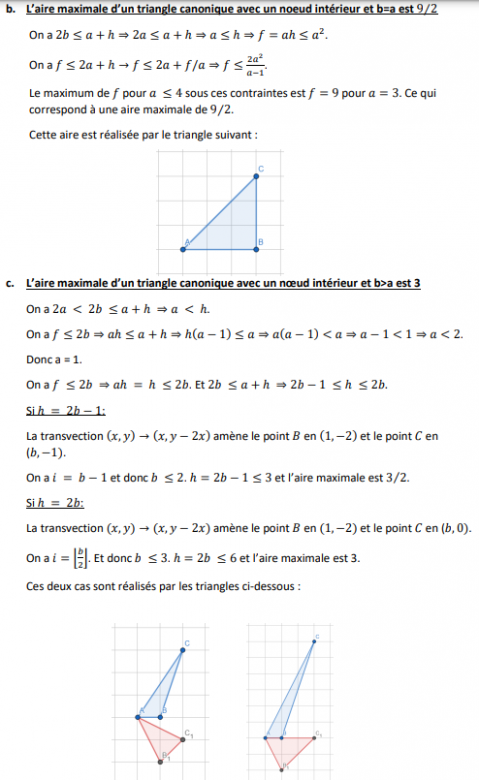
Lemme 4: Il n'existe pas de triangle canonique avec 2a < 2b <= h+a, un seul point intérieur et une aire > 9/2.
Il faudrait détailler l'inégalité: h = 2A = 2I + F - 2 = F <= 1+x+(1+x) = 2x+2. Et 2b <= h-a implique 2x+1 <= h.
Il faudrait préciser les transvections utilisées pour les deux cas particuliers.
Qu'en est-il du cas où x = 1 dans ces cas particuliers?
Lemme 5: Il n'existe pas de triangle canonique avec un seul point intérieur et une aire > 9/2.
Ce déduit des lemmes 2 et 4.
Lemme 6: Il n'existe pas de triangle avec un seul point intérieur et une aire > 9/2.
Ce déduit des lemmes 1 et 5.
CQFD.
Note: la transvection utilisée pour les deux cas particuliers pourrait être appliquée à n'importe quel triangle canonique avec 2a < 2b <= h+a pour obtenir le triangle (0;0), (a;-2a), (b; h-2b).
En effet, 2b-a <= h <= 2b.
De là on peut déduire que I >= b-1 = les segments (a;-a)(a;-2a) et (a;-a)(b;-a). Donc b <= 2, h <= 4, b > a >= 9/4 ce qui est impossible.
Ça remplacerait les lemmes 3 et 4.
Une fois le Lemme 2 complété alors la démonstration devrait être OK. Je pense 
Il est tout à fait normal d'avoir des approches différentes mais il est difficile de justifier ses affirmations quand elles sont incérées dans une démarche différente . Il n'y a pas d'erreur dans les formules données mais seulement des problèmes de lettres dans l'étape 1 .
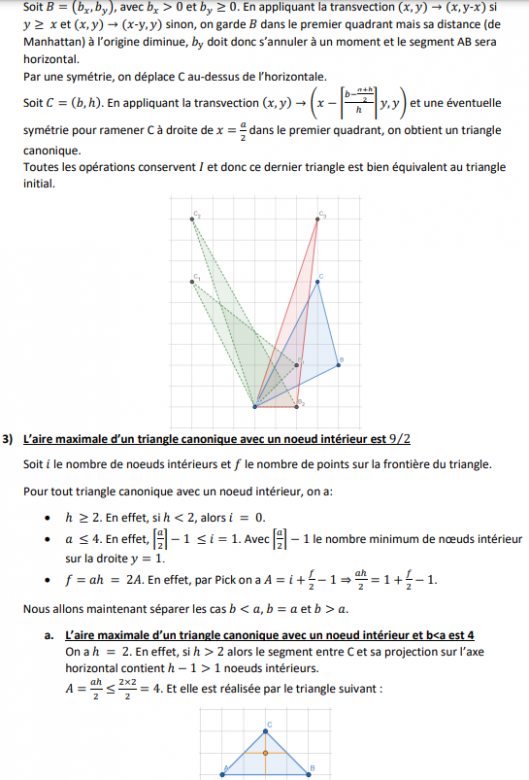
J'aimerais quand même justifier mon approche qui n'est pas dénuée de sens . On suppose l'existence d'un triangle avec une aire supérieure à 4,5 et on le "réduit" progressivement à un triangle ayant les mêmes propriétés pour exhiber une contradiction . Pour cela on utilise des transvections , c'est l'objet du préambule .
La première étape ne pose pas de problème , c'est un peu ton lemme 1 sauf que je ne m'intéresse pas aux dimensions . On veut simplement un côté porté par une ligne du quadrillage .
Pour la deuxième étape , je n'ai pas justifié le fait que C n'était pas à la verticale d'un point de [AB] car c'est de la géométrie élémentaire sachant que le triangle ne doit contenir qu'un seul point intérieur avec une aire supérieure à 4,5 .
L'inégalité 2x+1<=h n'est rien d'autre que 2x+a<=h de l'étape 2 . En effet si l'inégalité n'était pas vérifiée , on diminuerait x en envoyant le point C à gauche par la transvection .
Je ne suis pas sûr d'avoir répondu à toutes tes questions et remarques 
Imod
Voici ma version. L'approche est similaire mais j'étends les cas C au dessus de [AB] je te contredis dans le Lemme 4 pour x=1.
@malou, j'utilise le bouton Pdf mais ça n'affiche pas le pdf directement dans le post comme tu as fait plus haut.
PDF - 256 Ko
malou edit > ** en images deux messages plus bas pour ceux qui préféreraient **
Bonjour LittleFox, normal...c'est parce que plus haut j'ai fait des images avec le contenu du pdf
dites messieurs...ne savez-vous pas que normalement on ne peut pas poster ses recherches sous cette forme...allez, on est dans le forum détente et ce sont les congés, mais je ne voudrais pas que cela donne trop de mauvaises idées aux demandeurs d'aide "classiques"
allez, je vais te faire des images de ton pdf
@LittleFox : On est tout à fait dans ce que je disais , la rédaction est sans doute plus claire pour toi mais pas pour moi . Il y a beaucoup de choses en commun dans les deux approches mais j'ai tendance à privilégier la description aux calculs . Il me semble toutefois que tout est dit dans ma démonstration plutôt économe en formules 
Je vais commencer à regarder ( tranquillement ) le cas où il y a plusieurs points intérieurs .
@Malou : Je pense que tu as compris que je n'avais pas l'intention de gêner la modération avec mon message pdf et je crois que LittleFox est comme moi . J'ai passé un "petit" moment à rédiger mon pdf et j'ai renoncé à le transcrire avec le LaTex du site d'autant que le nombre d'images est limité . Le site propose de joindre un fichier sous la forme pdf et je ne voyais aucun mal à ça . Après on peut ( comme tu l'as fait ) transformer le pdf en image mais là je suis d'une nullité sans fond et je crains alors d'empoisonner bien plus la modération 
Imod