Annuler
connectez vous
- Cours sur les triangles : construction et droites remarquables - cinquième
- Exercices sur les nombres en écriture fractionnaire - cinquième
- Dix problèmes pour revoir les acquis de la sixième - cinquième
- Quatorze Exercices pour démarrer le calcul numérique - cinquième
- Seize Exercices portant sur le programme de cinquième
- Vocabulaire cinquieme
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. CinquièmeForum de cinquième TrianglesTopics traitant de triangles [tout]Lister tous les topics de mathématiques
Niveau cinquième
mesure angle
Posté par vali
Bonjour,j'ai commencé un exercice, pouvez-vous me dire si j'ai bon et m'aider, merci
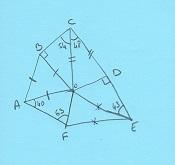
A partir des données de la figure, calculer la mesure de l'angle OEF
J'ai calculé les angles des triangles :
Triangle BCO rectangle en B
angle BCO+angleBOC = 90°
54+BOC=90
BOC=90-54=36°
Triangle BAO équilatéral BO=OA=AB=60°
Triangle AOF
40+63+X=180
103+X=180
X=180-103=77°
Triangle COD
X+X+48=180
2X+48=180
2X=180-48
2X=132
X=132/2=66° pour angles COD et CDO
Triangle DEO
angle DOE+DEO=90
DOE+43=90
DOE=90-43=47°
Triangle OEF est un triangle isocèle donc la somme des angles est égale à 180°mais comment faire pour calculer l'angle OEF ?
Bonjour Vali.
Tu as calculé cinq des six angles qui sont autour de O. Le sixième, EOF, vaut 360° moins la somme de ces cinq angles.
Angle OFE = angle EOF; angle OEF = 180° - 2 * angle EOF.
Attention : pour le triangle équilatéral, tu as cité les côtés au lieu des angles.
Bonjour,
360° c'est un tour complet par définition du degré
mais ! l'énoncé est un piège ! tout est faux dans ce problème (c'est fait exprès ?)
par exemple le triangle OEF n'est pas un triangle isocèle
en fait les données de l'énoncé sont redondantes : il y a une donnée de trop, qui est contradictoire avec les autres.
il est impossible d'avoir à la fois les angles indiqués, et tous les côtés indiqués égaux comme étant réellement égaux.
Soit un angle est donné en trop, soit une des indications de côtés égaux est fausse
preuve :
partant du segment OA on construit successivement
le triangle OAF (angles)
le triangle OAB (équilatéral)
le triangle rectangle OBC (angles)
le triangle isocèle OCD (angles)
le triangle rectangle ODE (angles)
et c'est fini !!! tous les points sont construits et l'information "OEF isocèle" n'a pas été utilisée. elle ne sert donc à rien et peut donc tout à fait être fausse, et d'ailleurs elle l'est, fausse !
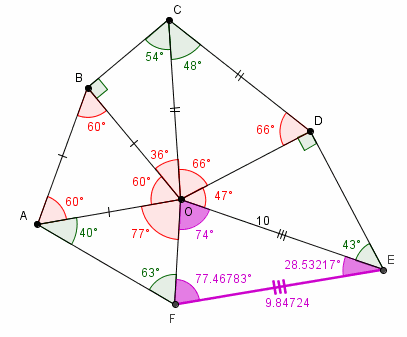
soit cette information "OEF est isocèle" est (volontairement) fausse
soit un des angles donnés est faux.
comment donc calculer les deux angles qui nous manquent OFE et OEF ??
sachant que le triangle OEF est désormais quelconque et pas isocèle pour un sou.
on a bien entendu immédiatement les angles E+F = 180° - 74° = 106°
mais ensuite ? le problème ne semble pas faisable au niveau annoncé
d'ailleurs la valeur "bizarre" des angles mesurés par Geogebra en est l'indication : on va obtenir des abominations avec des équations de degré élevé ou des fonctions trigonométriques.
donc autre hypothèse : c'est l'un des angles donnés qui est faux
ou bien COD pas isocèle, ou bien OAB pas équilatéral.
mais là on ouvre une infinité de possiblités de "modifier l'énoncé" pour le rendre juste et surtout calculable à ce niveau ...