Inscription / Connexion Nouveau Sujet
Mesure d'un angle dans carré + triangles équilatéraux
Bonjour,
Je bloque sur un exercice et j'aimerais avoir une petite aide :$ !
Voici l'énnoncé :
"Dans le carré ABCD, on construit les triangles équilatéraux directs ABF et CBE.
Figure (approximative) : 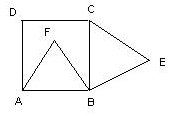
1) Donner une mesure de l'angle ( ;
)"
-------------------------------------------------------------------------------
J'ai déjà essayé en décomposant avec la relation de Chasles de différentes façon mai j'aboutit pas :s ! C'est surement quelque chose de simple que je ne vois pas... Si quelqu'un pourrait m'aider s'il vous plait ...
Je vous remercie
Bonne journée  !
!
édit Océane : image placée sur le serveur de l'
Merci beaucoup !!!!!!!!!
Par contre, je bloque encore sur une autre question :s :
"Donner une mesure de l'angle (;
) et en déduire une mesure de l'ange (
;
)"
Pour la première partie, j'ai réussi :
(;
) = (
;
) + (
;
)
= +
=
Mais pour en déduire (;
), je ne vois pas ...
Je vous remercie =)
je suis en premiere
bonjours a tous, j'ai exactement le meme exercice que toi florian0250 et je n'y arrive pas non plus.
j'aimerais savoir, sur ta figure le triangle AFD est isocele ????
je n'arrive pas a repondre a cette question : " determiner une mesure de l'angle (DF ; DE).
Que peut-on en deduire pour les points D, F et E ? "
MERCI DE VOTRE ATTENTION
bonjour
la relation de Chasles donne:
(FD,FE)=(FD,FA)+(FA,FB)+(FB,FE) (en termes de vecteurs)
= (
)
= (
)
les points D;E;F sont alignés
a bientôt
ce que tu viens de faire, c'est pour prouver que D, E et F sont alignés.
MAIS la mesure de (DF ; DE) c'est quoi.
Moi, j'ai ecrit que c'etait egal a 0. est ce juste ??????
bonjour
si les points sont alignés que peur valoir l'angle DF,DE
l'examen graphique confirmera la réponse que vous attendez
cordialement

 :)
:)
