Inscription / Connexion Nouveau Sujet
Modélisation
Bonjour, pouvez-vous me dire si mes réponses sont corrects svp
Vous êtes un ingénieur en mathématiques appliquées et une entreprise de jouets d'extérieur vous embauche pour aider à la réalisation de leur nouvelle gamme de toboggans. Le toboggan est constitué de deux parties, la première, pentue, qui permet aux enfants de prendre de la vitesse et la deuxième moins pentue, qui ralentit les enfants pour un atterrissage en douceur. La hauteur du toboggan est de 3 mètres. Après 2 mètres de descente, les enfants doivent se trouver à 0.5 mètre du sol.
Les deux parties sont modélisées par les fonctions suivantes :
Sur [0;1] : f1(x) = ax²+c
Sur [1;3] : f2(x) = d(x-2)³+e
Où x correspond à la distance au sol en mètres et a, c, d et e sont des réels. Votre buts est de trouver les valeurs de a, c, d et e pour créer un toboggan "harmonieux"
Partie 1: c et e
Déterminer les valeurs de c et e pour que votre toboggan respecte les caractéristiques fournies dans l'énoncé.
c= 3 car c'est la hauteur
e= 0.5 car c'est l'arriver du sol
Partie 2: Cas particulier
Dans cette partie, a= -0.5 et d= -2
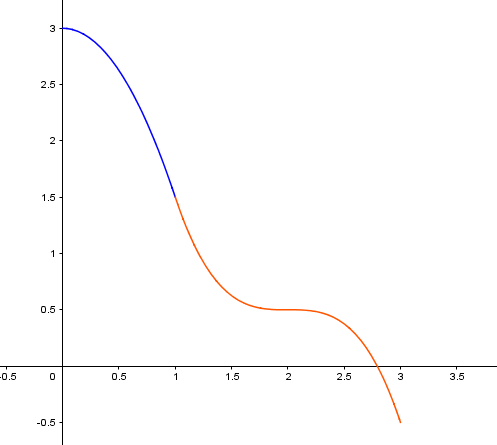
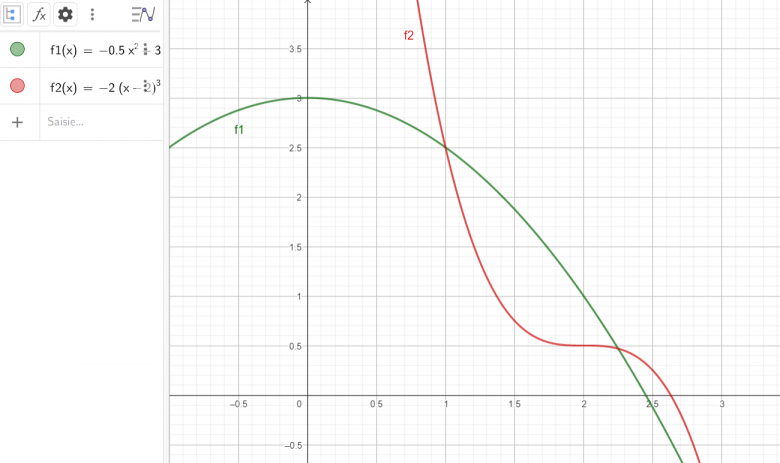
1. Sur la calculatrice ou sur Geogebra ou sur votre copie, tracer précisément les courbes représentatives des fonctions f1 et f2.
f1(x) = -0.5x²+3
f2(x) = -2(x-2)³+0.5
Voir pièce jointe.
2. Ce toboggan vous semble-t-il harmonieux? Lisse? Pourquoi ?
Non ce toboggan n'est pas lisse et harmonieux car on peut voir que au niveau de la jonction (1;2.5). La chute est pentue.
Partie 3: Construction du toboggan idéal
Trouver a et d pour qu'il n'u ait aucune différence de pente au niveau du raccordement des deux fonctions. Détailler votre démarche. Enfin, tracer dans un repère les courbes des fonctions obtenues.
Aide au calcul : (a-b)³ = a³-3a²b+3ab²-b³
Je ne s'ait pas comment faire pour cette question.
Bonsoir
Le texte est peu clair
À quoi correspond les deux mètres ?
Le point d'intersection des deux courbes doit avoir pour abscisse 1.
et les courbes doivent avoir une tangente commune en ce point
Bonjour hekla,
Le texte est peu clair
À quoi correspond les deux mètres ?
pour moi il me semble clair que les deux mètres correspondent au déplacement horizontal sur le toboggan au moment où il se termine à 0.5m du sol, au point B imposé. quelles que soient les valeurs des paramètres a et d
(ça ne peut pas être compté verticalement, ni le long du toboggan)
(figure mise ici car correspond à celle déja mise par Loulou2813)
ce qui n'est pas clair c'est que le toboggan modélisé vers sa fin par f2 continue après ce point là pour pénétrer dans le sol !
il aurait été logique d'arrêter f2 à 2m, dans[1; 2] au lieu de [1; 3]
(chercher le point S est hors sujet)
sur ce, je te laisse bien entendu poursuivre sur le fond du problème.
Bonjour mathafou
C'est bien ce que je pense aussi, mais il eut été préférable de le dire comme la position du toboggan, c'est-à-dire la position de l'origine du repère.
Je me demande aussi pourquoi la fonction est définie aussi sur
je me permets de relancer car après cet "aparté", la balle est bien dans le camp de Loulou2813
le travail à faire (par lui) étant
Le point d'intersection des deux courbes doit avoir pour abscisse 1.
et les courbes doivent avoir une tangente commune en ce point
Bonjour,
Est-ce que les parties 1 et 2 sont corrects ?
Pour la partie 3, je doit donc calculer la tangente des 2 fonctions au points d'abscisse 1 ?
en l'absence de hekla
Les équations de tangentes elles mêmes ne servent à rien du tout
(surtout que la deuxième est fausse)
on veut :
en x = 1 la même ordonnée (point commun entre les deux courbes, même y pour un même x)
ça se traduit comment ?
et on veut aussi en ce point x = 1 la même pente des tangentes
comment s'écrit la pente (juste la pente) d'une tangente en x = 1 ?
Bonsoir
Pourquoi 7,5 ? d'accord pour la tangente en 1 à la courbe représentative de
d'où
Il en résulte que l'équation de la tangente est
or
d'où
comme tu es revenu je te laisse poursuivre avec ta méthode.
bien que l'écriture des équations de tangentes me semble inutilement compliquée.
Je pensais écrire des équations de tangentes pour dire qu'en 1 les tangentes sont les mêmes donc égalité du coefficient directeur et égalité de l'ordonnée à l'origine.
Fais-je une erreur ?
Il faut donc calculer le point d'intersection des 2 courbes mais je n'arrive pas à le faire avec a et d manquant.
oui oui, c'est bon
je m'en suis aperçu après coup et j'ai rayé tout ce que j'avais dit.
on peut donc poursuivre avec ta méthode.
y=f'_2(x)(x-1)+f_2(x) or f_2(x)=d(1-2)^3+c=c-d=0,5-d
J'ai pas compris pour la partie f_2(x)
c est bien égale à 0.5, pourquoi on utilise c-d ?
à vous deux
désolé de la perturbation, mais 1h sans réaction de hekla j'avais mis une réponse
oublies et fais comme a dit hekla
(utilisation des équations de tangentes et traduire que c'est la même droite)
on pourra faire l'autre méthode (la mienne) ensuite
y=f'_2(x)(x-1)+f_2(x) or f_2(x)=d(1-2)^3+c=c-d=0,5-d
J'ai pas compris pour la partie f_2(x)
c est bien égale à 0.5, pourquoi on utilise c-d ?
C'est bon je viens de comprendre mon erreur, j'ai utilisé la fonction développé a lieu de la fonction de base.
effectivement, je viens de voir, sorry
Du coup, je trouve bien les 2 bonnes équations de la tangente.
Mais je en comprend toujours pas ce que je doit faire après
Écrire que c'est la même
coefficients directeurs égaux
même ordonnée à l'origine
si vous avez deux droites d'équation et
alors on doit avoir
ce sera bien la même droite.
En fait ce qui me bloque c'est que je comprends pas comment faire mon système avec les inconnues a et d
En détaillant
coefficient directeur de la tangente en 1 à la courbe de :
coefficient directeur de la tangente en 1 à la courbe de :
d'où première équation
Ah d'accord,
Du coup on a,
2a=3d
- a + 3 = - 4d + 0.5
a = (3/2)d
- (3/2)d + 4d = 0.5 - 3
a = (3/2)d
(5/2)d = - 2,5
a = (3/2)d
d = -1
a = - 3/2
d = -1
Est-ce bon ?
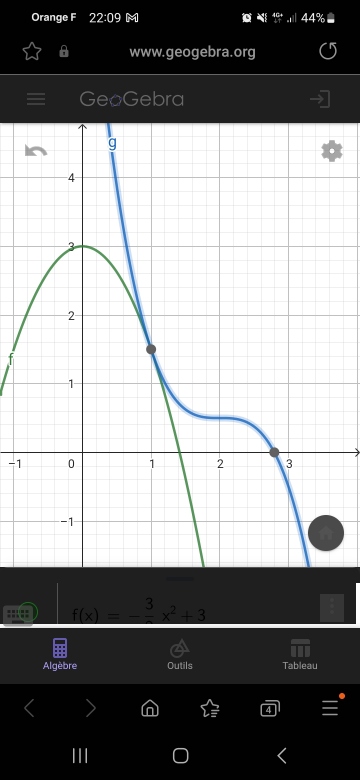
Du coup, sur je suis allez vérifier la pente sur geogebra, on peut voir qu'elle est harmonieuse et lisse même si elle paraît raide.
Pour une fonction, par exemple
on écrit elle est définie sur
sur un intervalle
f2(x)=Fonction(g,1,3) vous ne l'aurez que sur [1 ; 3] c'est ce que j'ai fait
21 : 03
ce sera encore plus visible
voila.
si on prenait au pied de la lettre "au point de raccordement il n'y a pas de rupture de pente"
Le point d'intersection des deux courbes doit avoir pour abscisse 1.
car c'est le seul point commun entre les deux intervalles de définition [0; 1] et [1; 3]) :
donc
f1(1) = f2(1)
(traduction de point commun = même abscisse 1 et même ordonnée y)
c'est à dire
a(1)^2 + 3 = d(1-2)^3 + 0.5
a+3 = -d+0.5
a+d = -2.5
même pente en ce point (alias coefficient directeur) :
f'1(1) = f'2(1)
2a*1 = 3d(1-2)^2
2a = 3d
et on a directement deux équations en a et d
la suite pareil : on résout ce système (équivalent à celui qu'on a obtenu par l'autre méthode)
Bonjour
Deux droites sont confondues si elles sont parallèles et ont un point commun.
Le parallélisme est assuré par l'égalité du coefficient directeur.
En écrivant l'équation de la tangente, j'ai pris comme point commun,
l'ordonnée à l'origine. Il est bien évident que le point d'intersection des
deux courbes est plus intéressant, car de toute façon, il faut calculer ses
coordonnées. Votre méthode est donc plus rapide et nécessite moins de
calcul.
ma méthode ne calcule pas directement le point commun C
j'écris juste que c'est le même dans les deux courbes
le but est d'obtenir a et d, rien de plus
ensuite si on reporte x = 1 dans l'une des deux équations de courbes obtenues (une fois le système en a et d résolu) on a les coordonnées de C, c'est pareil dans les deux méthodes.
j'économise juste l'écriture des équations de tangentes.
à mon avis les calculs se valent.
surtout si l'élève a comme réflexe immédiat de réciter le cours sur les équations de tangentes sans chercher à réfléchir sur la signification de l'énoncé (que veut dire "aucune différence de pente au niveau du raccordement")
à ce sujet la rédaction de la réponse à la question 2
2. Ce toboggan vous semble-t-il harmonieux? Lisse? Pourquoi ?
Non ce toboggan n'est pas lisse et harmonieux car on peut voir que au niveau de la jonction (1;2.5). La chute est pentue.
ce n'est pas que "la chute est pentue" (sic) c'est que la pente est différente à gauche et à droite au point de jonction
bref que cela forme un point anguleux en C : le toboggan n'est pas lisse
on est d'accord là dessus
l'abscisse, mais son ordonnée est au départ inconnue et on ne la connaitra que tout à la fin.
quoique ... mais c'est hors sujet : des propriétés purement géométriques des tangentes à une courbe de degré 3 permettent de construire directement la tangente commune, donc le point C d'abscisse 1 sur cette tangente
et ensuite seulement de chercher les courbes qui passent par ce point C là
ça permet à une appli Geogebra de déterminer géométriquement le toboggan optimal "sans aucun calcul" explicite)