Inscription / Connexion Nouveau Sujet
mon oncle
"quel age as-tu"demande eric à son oncle jeremie,professeur de mathématiques en retraite.
"mon age est égal au nombre de côtés dun polygone regulier dont tous les angles sont égaux à 175 degrés"
Quel est l'age de tonton Jeremie?
>fatanlie91 (Evry ?)
Qd tu dis "tous les angles", cette formulation est fausse.
Mais on comprend ce que tu veux dire
Philoux
Bonjour fatanlie (Evry ?)
Plutôt que tout expliquer, inspires-toi de l'énigme ici, en cliquant sur la maison verte : ![]() Le polygone.
Le polygone.
Cette énigme est très proche de la tienne
Si ce n'est tjs pas clair, reviens
Philoux
Ok fatanlie
la valeur de 175° ne peut pas correspondre à un secteur isolé de ton polygone régulier puisque 2*175=350 et 3*175 fait plus de 360°.
par contre, Y a-il un nombre entier de ces secteurs de 175° qui puisse faire un nombre entier de tours de cercles ?
c'est cette question qui, je l'espère, peut te faire comprendre qu'on va chercher 2 nombres:
n = nombre de secteurs de 175°
k = nombre de tours de cercles faits avec ces secteurs
Donc on écrit :
n.175°=k.360°
et on cherche les plus petits nombres entiers n et k qui vérifient cela puisque n correspond à l'âge de Jeremie.
Tu ne peux que diviser par 5 ces chiffres 175 et 360, il n'y a pas d'autres multiples communs; cela donne :
35.n=72.k
les entiers les plus petits qui vérifient cela sont =
n=72 et k=35
il y aurait, bien sûr, tous leur multiples
n=144 et k=70
...
Mais puisque n est un âge, ce ne peut être que 72 (comme dit à 11:02)
As-tu compris ?
Bon courage
Philoux
J'aurais essayé !
Peut-être d'autres mathîlien(ne)s auront une autre méthode plus accessible pour toi.
A+ sur l'
Philoux
Bonsoir !
D'après ce que j'ai compris ...
Pour un triangle équilatéral : pas de problème : .
Pour un carré : pas de problème non plus : .
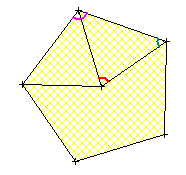
Pour un pentagone régulier ... là il faut un peu calculer  :
:
l'angle au centre vaut : (angle représenté en rouge). On a un joli triangle isocèle donc les angles à la base valent chacun :
(angle représenté en vert). Angles adjacents : l'angle en violet mesure
.
Pour le cas, général ( côtés), l'angle au centre mesure, en degrés,
. Les angles à la base de chaque triangle isocèle élémentaire mesure donc
. Et comme il faut multiplier ensuite par
pour obtenir l' "angle", on obtient alors :
.
Ton problème revient alors à résoudre l'équation d'inconnue suivante :
En multipliant par de chaque "côté" :
_____________________
Je suis nul en maths.
reBonsoir !
Pour ce qui est du niveau ... c'est limité pour une classe de cinquième ... la résolution d'une équation de ce genre se fait plutôt en 4e si je me souviens bien. :p ... mais faisable.
_____________________
Je suis nul en maths.
cest mon prof de math ki nou a donner tout une feuille de problemes (je suis totalement desesperer)
mais pour le probleme,pourkoi à tu fais un pentagone comme figure?????
reBonsoir
J'ai fait un trois cas particuliers : 3 côtés puis 4 côtés puis 5.
>>> Pour tenter de comprendre le "mécanisme".
Ensuite, le cas général.
_____________________
Je suis nul en maths.
rereBonsoir
Pour mon cas particulier conçernant le pentagone, j'ai bien entendu pris un pentagone régulier. J'obtiens ainsi 5 triangles isocèles superposables (tu veras en seconde que l'on appelle ça des "triangles isométriques").
C'est ce qui me permet de calculer l'angle au centre en divisant un angle plein en 5 "parties égales" d'où le calcul .
_____________________
Je suis nul en maths.
daccord je pense que ccest bon mais cest dur à expliquer...
rerereBonsoir
Surtout, il faut prendre une feuille, un crayon et faire les figures en même temps que tu lis.
Il ne faut surtout pas hésiter à "gribouiller".
Et recommencer jusqu'au moment de trouver (au collège on ne donne pas des choses impossibles, mais dans ton cas, pour un niveau 5e, ça me paraît un peu limite, mais bon, tout à fait possible; il doit y avoir plus simple ... mais il faut tout écrire  et c'est ça est "dur à expliquer" comme tu dis)
et c'est ça est "dur à expliquer" comme tu dis)
Si on ne trouve pas ... on remet ça au lendemain. 
_____________________
Je suis nul en maths.



