Inscription / Connexion Nouveau Sujet
Notation d'une fonction
Bonsoir, voici le problème:
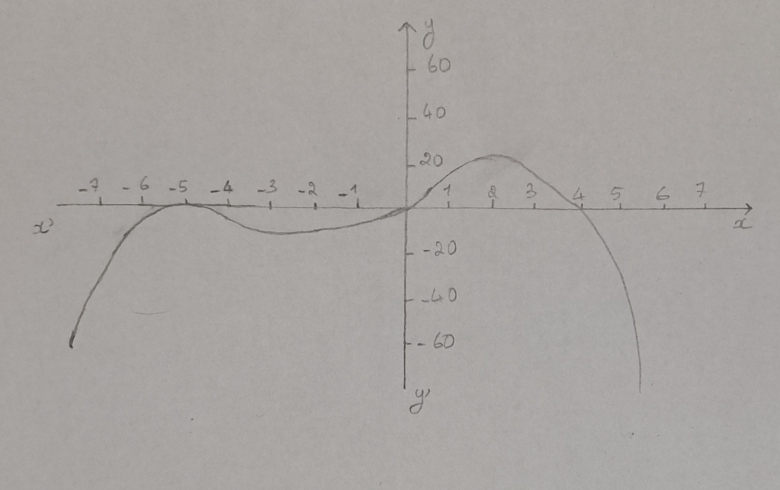
Quelle équations parmis les suivantes est celle de la fonction représentée dans le repère xy.
(Il y a plusieurs equ. par elimination il reste ces deux)
A:
B:
Je sais que B est la bonne réponse mais je ne sais pas pourquoi. Pourquoi le carré? Pourquoi pas le premier degré dans A?
Bonjour
Que pouvez-vous dire de la courbe au voisinage de -5 ?
Que pensez-vous de l'axe des abscisses ?
Je remarque que sur (x'O] la courbe ne dépasse en aucun point l'axe des abscisses. Elle touche -5 me ne le dépasse pas.
Il faut attendre au point (0;0) pour que la courbe a une ordonnée positive.
Alors pour l'algèbre dans la dérivée oui, mais pour les représentations graphiques on n'a pas encore commencé.
Oui on a commencé avec les tangentes, les deux demi-tangentes en notion, mais pas en pratique avancée.
Non
si vous avez un extremum la dérivée est nulle et la tangente est parallèle à l'axe des abscisses
C'est dans votre cours ou il y sera.
Vous ne voulez pas dire que l'axe des abscisses est tangent à la courbe
donc et c'est bien la B, parmi les deux proposées qui vérifie cette propriété.
D'accord, pour vérifier, je développe l'équation de B et je trouve sa dérivée. Ensuite je remplace x par -5. Je dois avoir 0 c'est ça?
Si vous voulez, mais il n'y même pas besoin
puisque vous avez un carré, la dérivée aura comme terme et les autres
donc pour
la dérivée sera nulle
Si, c'est bien ce que je disais. Vous avez
Si vous dérivez, vous obtiendrez
En donnant la valeur à
, vous obtiendrez bien 0
Bonjour,
Maintenant que le sujet est traité, je me permets de suggérer une variante :
regarder le signe de chacune des 2 fonctions quand
Bonsoirhekla,
Racines doubles, oui, j'ai bien vu, mais avoir ce réflexe en première ne me semble pas évident. 
Bonjour,
Je tombe par hasard sur ce sujet et propose une démonstration niveau seconde sans notion de dérivée ni de limite, ni de racine double :
Avec , on a par exemple
.
Or le point de la courbe d'abscisse -6 a un ordonnée négative.
J'ai choisi -6, mais on peut utiliser d'autres valeurs.
Le plus "intuitif" serait peut-être d'étudier le signe de la fonction f du A.




