Inscription / Connexion Nouveau Sujet
Octogone et carré
Bonjour,
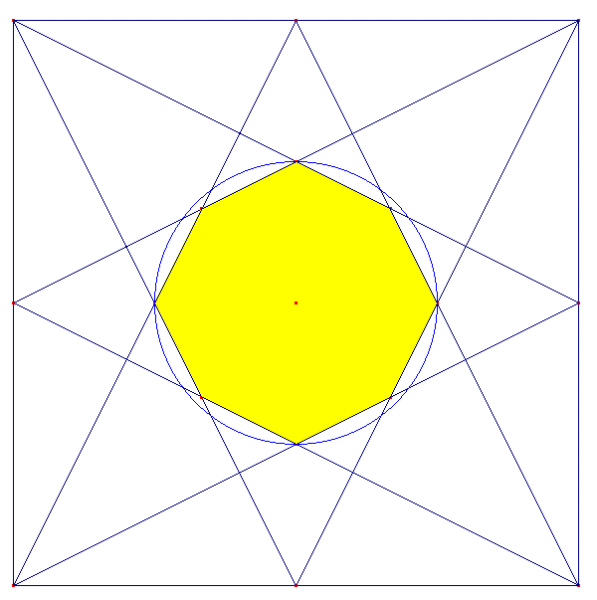
Dans un carré de 12cm, on a tracé comme le sous entend le dessin les segments joignant les sommets aux milieux des cotés
On demande simplement de trouver et justifier l'aire de l'octogone régulier ainsi construit.
Merci
Mince je suis grillé 
Merci pour la figure
Voici ce que je viens de trouver:
Première remarque: l'octogone n'est pas régulier !
Soit le carré de sommets (6,6),(-6,6),(-6,-6),(6,-6)
On découpe l'octogone en huit triangles superposables au triangle OAB avec A(2,2) et B(0,3) (il faut faire un peu d'analytique ici)
Ce triangle a pour aire S=(1/2)OA.OB.sin(AOB)=3
L'aire de l'octogone est donc 3.8=24 soit 1/6 de l'aire du carré.
L'octogone pas régulier?
Pourtant il donne l'impression, je ne sais pas comment je vais l'annoncer à mon prof
Et pourquoi utiliser les coordonné, je ne comprend pas ta technique.
Merci d'avoir répondu.
Fais une figure dans le repère indiqué (voir coordonnées des points)
Si tu as Geogebra sous la main c'est parfait. Personnellement je préfère travailler avec un logiciel de calcul formel (quel fainéant !)
A1(6,6),A2(0,3),A3(-6,6) etc dans le sens trigo
équation de (A2A7) et (A3A8), A leur intersection. On trouve A(2,2)
équation de (A1A4) et (A3A8), B leur intersection. On trouve B(0,3)
Le triangle (OAB) a un angle pi/4 compris entre 2 côtés 2sqrt(2) et 3. Son aire vaut 3 (à démontrer)
L'octogone est composé de 8 triangles de ce type.
Remarques:
1/ je ne trouve pas de solution élégante à ce pb, il doit bien y en avoir une !
2/ Joli piège cet octogone n'est pas régulier, ses angles ne sont pas égaux
un angle sur deux vaut 2.214,l'autre 2.498 exactement 2*atan(2) et pi-atan(3/4)
équation de (A2A7) et (A3A8), A leur intersection. On trouve A(2,2)
équation de (A1A4) et (A3A8), B leur intersection. On trouve B(0,3)
Je ne me souvient pas d'avoir fait ce genre d'équation, je ne la comprend même pas.
Tout ce que tu me dit est nouveau (ne t'inquiète pas je connais quand même le cercle trigo).
Mais si tu connais
A2 et A7 sont 2 points
tu cherches l'équation de la droite passant par ces deux points
Idem avec la droite passant par A3 et A8
Ensuite tu cherches le point d'intersection de ces deux droites
On le fait en seconde alors en première ...
Un petit coup de pouce ?
Je te conseille de faire un dessin à la main.
Soit A2(0,6) et A7(6,-6)
La droite (A2A7) a pour équation y=-2x+6
Soit A3(-6,6) et A8(6,0)
La droite (A3A8) a pour équation y=-x/2+3
L'intersection de ces deux droites est A(2,2)
Pour démontrer que l'angle est de pi/4:
Cos A et Sin A sont égaux à 2/3 (comme le cercle fait 3).
Ça tient la route?
Souviens toi que l'octogone n'est pas régulier
comme l'a bien montré caylus les points ne sont pas tous sur le cercle
Une fois ton dessin réalisé (à la main c'est très rapide) le triangle qui nous intéresse est OAB (voir coordonnées un peu avant)
Dans ce triangle l'angle AOB vaut pi/4 puisque A est sur la bissectrice du repère, les côtés se calculent facilement. Puis l'aire.
Attention ce triangle n'est pas rectangle.
L'aire du triangle OAB est de 3.
mais pourtant je trouve cette même aire pour les autres triangles ce qui fait une aire totale de 24.
Et geogebra m'indique aussi une aire de 24, donc j'ai raison?
Oui l'aire de l'octogone est 24 (8 fois 3)
Mais attention toutes les conjectures faites sur Geogebra doivent être démontrées en particulier l'aire de OAB doit être prouvée.
Si tu trouves une démonstration purement géométrique, sans passer par les coordonnées je suis preneur.
Maintenant il faut annoncer à ton professeur que l'octogone n'est pas régulier 
En passant retiens qu'un polygone équilatéral (ayant ses côtés égaux) n'est pas nécessairement régulier et donc n'est pas nécessairement inscriptible dans un cercle. Penser par exemple à un losange.
Pour OAB J'ai juste utilisé la formule de l'aire: base*hauteur
Comme B(0;3) OB=3 et A(2;2) hauteur=2
C'est pas assez?
Et je ne vois pas comment annoncé que l'octogone n'est pas régulier.
Oui base.hauteur/2 j'avais indiqué plus haut la formule S=1/2bcsinA totalement inutile ici. Comme quoi on est meilleur à 2 !
Tu dis simplement à ton prof que sur ton dessin on dirait bien que l'octogone n'a pas tous ses sommets sur le cercle
Mais il est plus que probable qu'il se sera aperçu de l'erreur.
C'est un farceur ton prof ?
C'est vrai que sur ton dessin initial approximatif on a tendance à postuler la régularité de l'octogone et on arrive à des contradictions.
Au final: excellent exercice de recherche.

 )
)
