Bonjour,
Quelle figure obtiens tu si tu coupes le cone par un plan vertical?

Je ne comprends pas ton dessin....

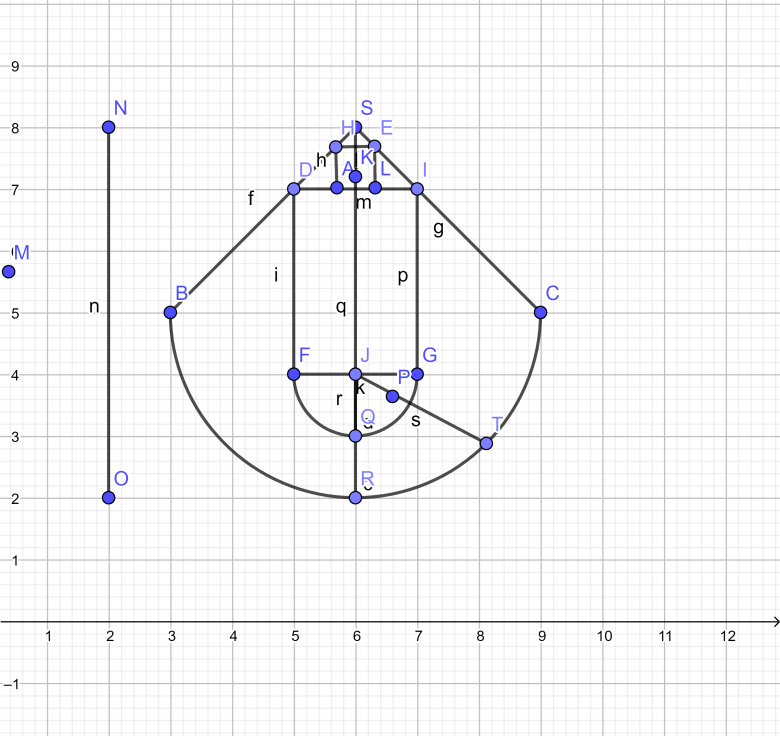
Ma figure c'est deux cylindres superposés le plus grans est le flacon de 3cm de rayon et le plus petit est le bouchon.
Ce flacon est inséré dans un cône de rayon R. La hauteur h u cône est de 5cm

grand
la hauteur h du cône

Apparemment ,il n'y a aucun renseignement sur le bouchon et je en comprends toujours pas ton dessin . Essaie de repondre à ma question.

Je sais que je ne dois pas envoyer de photos, mais je ne peux pas faire autrement en ce moment ((problème de matériel).
Parailleurs, je copié le texte intégral du problème.

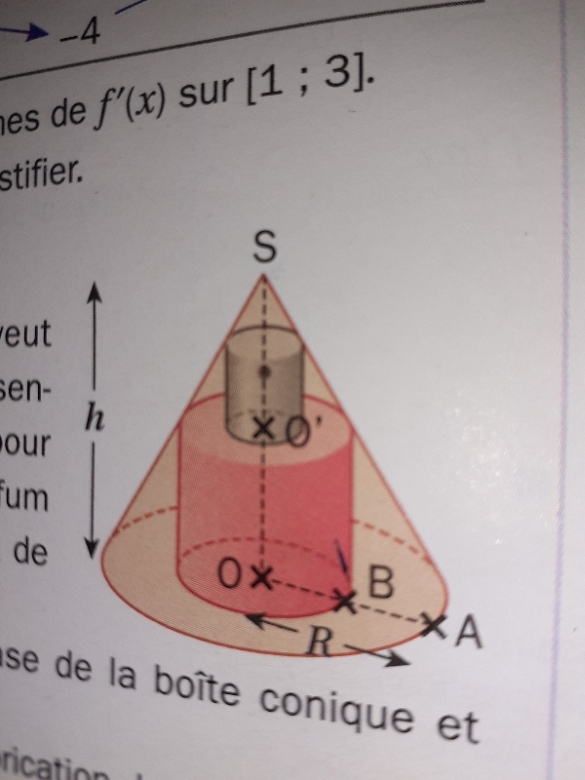
e peux calculer l'hypothénuse SB du triangle rectangle SOB  
SB =

Je peux calculer le volume du cône SOB
V = 84cm³

Le volume du cône SOA est
V =

Bonjour,
Apparemment il y a des erreurs dans ton énoncé.
Tu écris « La hauteur h du cône est de 5cm » à 12h26.
Or on ne connaît pas la hauteur du cône. Les 5cm correspondent à la hauteur du flacon en forme de cylindre.
Un petit dessin devrait  t'aider à calculer h en fonction de R.
On a O'C = 3 cm, O'O = 5 cm, SO = h, OA = R
Si tu utilises Thalès dans le triangle SOA, tu devrais y arriver.

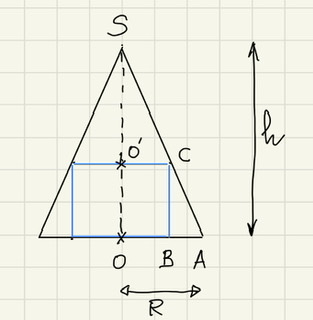
Ma difficulté est venue de mon erreur dans la lecture de hauteur
de 5cm.

5R = 3h

h = 4,24

V = 7,9 cm3

OO' / SO = O'C / OA = SC /SA
5 / h = 3 / R = SC / SA

SO'/5 = 3 / R

15 = SO'R

Comme je ne connais pas d'autres valeurs  

Attention SO ne vaut pas 5.
Quant à SO' c'est égal à SO - O'O.
SO = h et O'O = 5

SO'/h = 3/R
SO-5 / h = 3 / R
3h = R(SO-5)

Je viens de te dire que SO = h (hauteur du cône). Alors pourrais-tu l'utiliser ?
Ainsi tu auras h en fonction de R comme demandé dans l'énoncé.

h-5/h = 3 / R

R =3h/h-5

V = (3H/h-5)²)h/3
v = (9h²/h²-10h+25)h/3
V = (9h³/h²-10x+25)/3

V = (9h³/h²-10h+25)/3

Kikipopo, tu n'es pas assez attentive.
Dans l'énoncé il est demandé :
a. compte tenu des contraintes, exprimer la hauteur de la boîte conique en fonction de R.
En déduire le volume V en fonction de R.
Toi, tu as fait en fonction de h.
Alors tu recommences et tu fais ce qu'on te demande.

h=R(h-5)/3

V = [((Rh-5R)²/3)(Rh-5R)]/3

je ne vois comment éliminer le h

je ne vois pas comment substituer

V = [((5R/(R-3)²)(5R/(R-3)]/3
V = 125R³/R³/3+R²+R-3

Kikipopo, tu dois faire attention à ce que tu écris.
On a V= (/3)*R²*h
Et on a h = 5R/(R-3)
tu dois remplacer h par sa valeur dans V= (/3)*R²*h

Lorsque tu auras V en fonction de R, tu devras étudier cette fonction pour trouver la valeur de R qui minimise V.
Moi, je vais me reposer .

V = (/3)R²*(5R/R-3)
V = (/3)(5R³/R-3)

Merci beaucoup.
Je reprendrai demain.
Bonne nuit.

Bonjour,
V' = 15R²
R = 15
R 3
R =3,87

H = (3,87*5)/(3,87 -3)= 22,2

V =[( /3)(15*22,2)]/3 =349,3 cm³

V' = (/3)(15R²/1-3)

(/3)(((3R²(R-3)) - R³)/(R-3)²
(/3)(2R³-9R²/(R-3)²
(/3)(6R²-18R)/(R-3)²

{[(/3)((6R(R-3))]/(R-3)²
V' =(/3)(6R))/(R-3)
V' =(/3)(6R²-18R)

Excusez-moi, je m'étais absentée en toute fin d'après-midi parce que les messages ne me parvenaient pas.
V' = (5/3)*((3R²(R-3)-R³/(R-3)²
V' = 5/3 (2R^3-9R²)/ (R-3)²

Je ne vois pas quoi faire d'autre pour trouver la valeur de R

V' est correct.
Pour déterminer un extrémum de V il faut déterminer R pour lequel V' s'annule.
Donc ici,  2R³ -9R² = 0
Soit R²*(2R-9) = 0
A toi de conclure pour trouver R. N'oublie pas que R est différent de 0.

Si un  produits de facteurs est nul au moins l'un des facteurs est nul.

R2 * (2R-9) =0
R

3

V = [*(4,5)²*15]/3
V = 318 cm³

Bonne soirée et à bientôt sur l'

Ma calculatrice me donne 318, 08625618. Ce doit être en fonction de la précision de
Merci beaucoup.
Bonne nuit
Bientôt

Tu as raison. J'avais pris 3,14 pour la valeur de .
En prenant une valeur plus précise, on a bien les 318 cm³ que tu as indiqués.
Excellente remarque de ta part.
Bonne nuit.

Rectification : si tu trouves 318,086 pour V, la valeur arrondi au dixième près devient 318,1 cm³