Inscription / Connexion Nouveau Sujet
Optimisation
Bonjour j'ai un problème sur un exercice :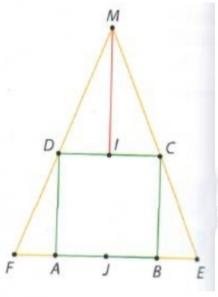
* modération> Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum maroui,  *
*![]() A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI (Clique sur ce lien)
A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI (Clique sur ce lien)
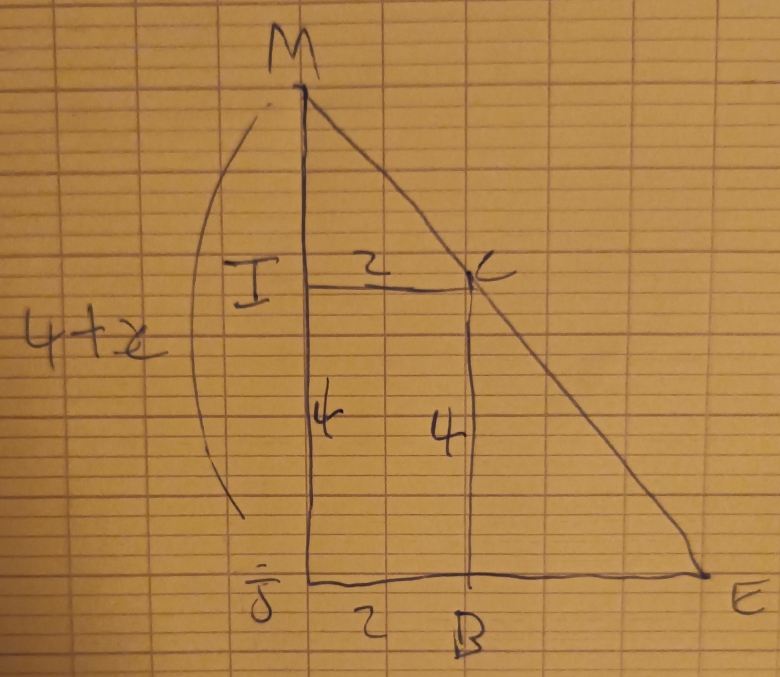
On pose IM=x.
A quelle intervalle appartient le réel x?
]0;+infini[.
Exprimer la hauteur du triangle MEF en fonction de x et la longueur de EF en fonction de EJ.
Reponse : hauteur MEF = 4+x
Et EF=2EJ
Bonjour maroui
tu n'es pas nouveau pourtant...mais tu n'as pas respecté le règlement pour les images
Recopie ton énoncé s'il te plaît, ensuite quelqu'un pourra te venir en aide

Un architecte doit décider des dimensions de la façade d'un chalet.
Il estime que la partie utilisable, pour placer les fenêtres et les
portes est un carré de côté 4 m.
Pour des raisons esthétiques, la façade est choisie isocèle en son
sommet le plus haut.
On modélise la situation par le carré ABCD, de côté 4, et le triangle MEF.
I est le milieu du segment [CD] et J est le milieu du segment [AB].
M est un point de la médiatrice du segment [CD], situé au dessus de [CD].
Les droites (MC) et (MD) coupent la droite (AB) respectivement en E et F.
On se propose de déterminer la valeur minimale de l'aire du triangle MEF
Non.
Dessine au brouillon uniquement les parties de la figure qui t'interessent pour appliquer THALES.
Q4) On considère la fonction f définie sur l'intervalle ][ par f(x)=(2(x+4)²)/x.
À l'aide d'un logiciel de calcul formel on a obtenu ci contre l'expression factorisé de f'(x).
Justifier le résultat

Une remarque :tu peux partir de la forme factorisée du numerateur sans la developper pour deriver si tu as vu en cours la dérivée de un