Inscription / Connexion Nouveau Sujet
parallélépipède rectangle
Salut,
J'ai un DM à rendre mais je le comprend pas.Pourriez-vous me l'expliquer?Voilà l'énoncé:
1) Calculer les volumes de ces deux réservoirs afin de monter qu'ils ont le même volume.(rappel:la longueur L, la largeur l, et la hauteur h d'un parallélépipède rectangle sont les longueurs des arêtes issues d'un même sommet.Le volume d'un parallélépipède rectangle est: V= L*l*h.
2)On remplit en même temps les deux réservoirs grâce à deux robinets qui fournissent la même quantité d'eau chaque seconde. Un des deux réservoirs sera-t-il rempli en premier? Pourqoi?
3)Dans quel réservoir l'eau montera le plus vite dans un premier temps? A la fin? Pourquoi?
Merci à tous.
Bonjour thalie13
Ta figure n'est pas très explicite
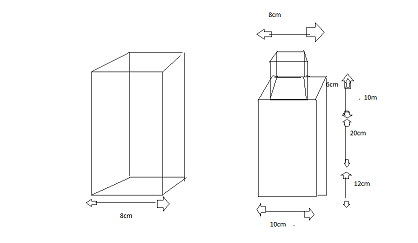
La base du réservoir de gauche est-elle 8 cm*12 cm et sa hauteur 20 cm ?
La base de celui de droite est-elle 10 cm*12 cm et la hauteur 20 cm ?
La partie supérieure de celui de droite, base 5 cm*5 cm et hauteur 10 cm ?
Tu dois préciser ça clairement
Bonsoir,
Désolé de n'avoir pas répondu plutôt,le 1er grand réservoir: largeur=8 cm
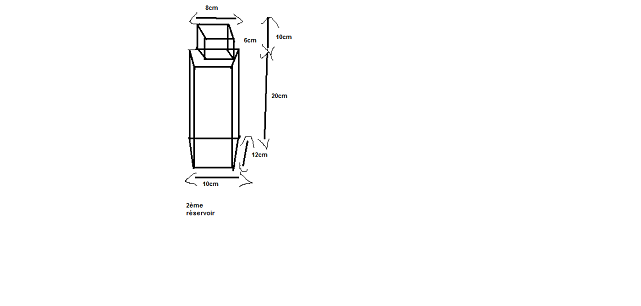
Le 2ème réservoir:
Grand parallélépipède rectangle:
largeur=10cm; longueur=12cm; hauteur=20cm
petit réservoir posé dessus:
hauteur=10cm; longueur=6cm; largeur=8cm
Je suis désolé pour la figure, j'ai fait ce que je pouvais. Merci pour votre aide, j'ai de gros problème avec cet exercice.
Désolé de n'avoir pas répondu plutôt,le 1er grand réservoir: largeur=8 cm
Ce serait plutôt plus tôt
8 cm n'est pas une nouveauté c'est marqué sur le dessin, mais l'autre dimension de la base et la hauteur ?
Tes cotes sont tout juste lisibles
Pour le second réservoir c'est bien:
base 10*12 cm, hauteur 20 cm et pour le "goulot" base 8*6 cm hauteur 10 cm
Confirmes
Non tant que tu ne m'auras pas donné les dimensions que je t'ai demandé pour le réservoir de gauche (ça fait 2 fois que je te demande ça)
Bonsoir Mijo,
Sur le réservoir de gauche,le professeur nous a donné que la mesure de la base=8cm. Par contre,la longueur du réservoir de gauche et de droite +bouchon sur le schéma ont la même taille.Il n'y a que la base qui diffère, la largeur du résevoir de gauche est plus petite que celle de droite.
Réservoir de gauche base=8cm et reservoir de droite base=10cm j'ai reproduis le schéma et ses dimensions. Je n'ai pas plus d'information.
Est-ce que cela pourrait-être:
réservoir 2:
V=10*12*20=2400cm3 et volume bouchon=8*6*10=480cm3
donc volume base+bouchon=2400+480= 2880cm3
réservoir 1:
D'aprés le schéma, il est aussi grand que le réservoir 2(base+bouchon) et s'ils ont la même longueur donc:
V= 8*12*(20+10)= 8*12*30= 2880cm3
donc réservoir 1 et 2 même volume.
Pour la deuxième question,là je ne vois plus!!
Pouvez-vous m'aider
bonjour,
n'as-tu pas une indication comme volume de gauche est un pavé de base carrée!!!
ok volume réservoir de droite V2=2400+480=2880 cm^3
Coucou,
Non les deux réservoirs sont des parallélépipède rectangle d'après l'énoncé.
J'ai essayé de reproduire la figure comme j'ai pu.Sur le premier réservoir,il n'y a pas plus d'indication.En ce moment on étudie la proportionalité!D'après la figure sur le schéma, ils ont tous les deux la meme hauteur mais pas la même largeur.J'ai donné toutes les indications que j'avais.
2)On remplit en même temps les deux réservoirs grâce à deux robinets qui fournissent la même quantité d'eau chaque seconde. Un des deux réservoirs sera-t-il rempli en premier? Pourqoi?
si les réservoirs ont le même volume, ils se rempliront dans le même temps
sinon, le réservoir de plus grand volume sera rempli moins vite
c'est tout ce qu'on peut dire
3)Dans quel réservoir l'eau montera le plus vite dans un premier temps? A la fin? Pourquoi?
Merci à tous.
de même cela dépend de la surface de la base!!
plus la surface de la base est grande, plus l'eau mettra de temps à monter dans le réservoir à volume égal
1) Calculer les volumes de ces deux réservoirs afin de monter qu'ils ont le même volume
Enfin on apprend déjà une chose, les deux réservoirs ont la même hauteur 30 cm
On n'a qu'une des 2 dimensions de la base du réservoir de gauche, supposons que celle qui manque est 12 cm
Son volume est alors V1=8*12*30=2880 cm³, donc le même que l'autre
2)On remplit en même temps les deux réservoirs grâce à deux robinets qui fournissent la même quantité d'eau chaque seconde. Un des deux réservoirs sera-t-il rempli en premier? Pourquoi?
Comme les 2 volumes sont identiques, le volume à remplir avec le même débit prendra le même temps
3)Dans quel réservoir l'eau montera le plus vite dans un premier temps? A la fin? Pourquoi?
Le premier temps correspond à la montée de l'eau sur une hauteur de 20 cm (jusqu'à atteindre le goulot de celui de droite)
1 er temps
Volume de celui de gauche Vg=8*12*20=1920 cm³
Volume de celui de droite Vd=10*12*20=2400 cm³
Pour cette partie l'eau montera plus vite dans le réservoir de gauche puisque son volume est plus faible
Pour la partie restant à remplir dans un 2 ème temps
Le volume pour celui de gauche est 8*12*10=960 cm³
Pour celui de droite 8*6*10=480 cm³
Pour cette partie l'eau montera 2 fois plus vite dans le réservoir de droite que dans le réservoir de gauche, puisque le volume à remplir est 2 fois plus petit dans celui de gauche
Cependant le remplissage complet des 2 réservoir prendra le même temps
Si on appelle D le débit commun aux deux réservoirs
Pour le réservoir de gauche le temps de remplissage total sera Tg=1920/D+960/D=2880/D
Pour celui de droite
Td=2400/D+480/D=2880/D
Donc Tg=Td

 3
3
