J avais pensé à faire d'abord le patron d'un cube puis faire les troncatures sur ce patron mais ça ne marche pas.

Y a personne qui pourrait m'aider?

Bonsoir nuit d'étoiles

J'essaierai de te faire un dessin demain.

Pour ta réflexion :
Que devient une face du cube quand on enlève ainsi les tétraèdres ? Et il y a 6 faces dans un cube...

Que devient un sommet du cube quand on enlève les tétraèdres ? Et il y a 8 sommets dans un cube...

Bonne réflexion !

Bonjour Coll,

J ai fait la figure du cube puis j ai enlevé les tétraèdres,
La face du cube devient, je pense, un carré. (mais faut que je le démontre)
Et le sommet du cube devient, un triangle. Je pense, pas quelconque. (mais là encore faudrait le démontrer.)
Au total, je trouve que la figure a 14 faces et 12 sommets.

Tout ce que tu as écrit est correct.

En effet le polyèdre a 12 sommets, 14 faces, dont 6 carrés et 8 triangles (qui ne sont pas quelconques).
Je pense que les démonstrations sont simples ; mais tu peux les poster.
Que vaut le côté d'un carré ?
Que vaut le côté d'un triangle ?

J'ai des figures qui attendent tes réponses...

Ok.

Pour le côté d un carré, je trouve que c est égal à environ 2.1 cm.
Pour le côté d un triangle, je trouve la même chose puisque ses côtés sont confondu avec ceux des carrés. (on peut donc dire que ce sont des triangles équilatéraux)

Le côté du cube valant 3 cm (par exemple EF = 3 cm) une diagonale d'une face (par exemple EG) vaut
et donc le côté du carré qui reste dans une face après troncature des sommets vaut la moitié de cette diagonale c'est-à-dire


Tu as raison, les 8 triangles qui remplacent les anciens sommets du cube sont des triangles équilatéraux qui ont bien un côté égal à celui des nouveaux petits carrés.

Le cube de départ :



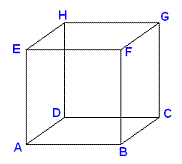
On en aura besoin pour les noms des sommets et des faces.
Je numérote ainsi les faces :
ABCD : 1
ABFE : 2
BCGF : 3
CGHG : 4
DAEH : 5
EFGH : 6

Voici ce qui reste de la face 6 après toncature avec les quatre triangles équilatéraux qui remplacent les sommets E, F, G et H



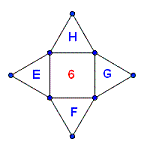
Il faut maintenant continuer de proche en proche. Il n'y a pas une solution unique mais il y a un grand nombre de solutions. J'en posterai une mais j'attends d'abord de te lire pour savoir si tu y arrives.

Euhm...

J avais pensé faire la même chose avec la face 1:
E => A
F => B
H => D
G => C

Mais il manquerait les 4 autres carrés.

Peu importe, tu peux commencer par la face 1 entourée des quatre triangles équilatéraux pour A, B, C et D.
Mais le problème consiste à continuer ensuite, c'est-à-dire à placer maintenant les faces latérales (faces 2, 3, 4 et 5) le long des bons côtés des triangles équilatéraux ; puis enfin la dernière face (la face 6 si tu commences par la face 1 ou la face 1 si tu commences par la face 6).

Il te sera très difficile de m'expliquer sans poster une figure. Sais-tu poster une figure ? L'as-tu déjà fait ?

Non je ne l'ai jamais fait et je n ai pas de logiciel de géométrie.
Je sais pas si je peux utiliser autre chose.

Ce n'est pas mon habitude de donner la solution, mais... pour Noël et les vacances, je vais faire une exception



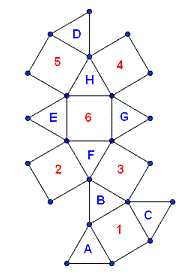
Comprends-tu cette solution (il faut peut-être y passer un peu de temps...) ?

Oh! Je n'étais pas loin, mais je me suis embrouillé dans les lettres, ce qui donné quelque chose de pas très cohérent.

Merci

(Avec quoi fais tu les figures?)

Je fais certaines figures avec Paint

Mais pas les trois figures de ce topic :
Je les ai faites avec Geogebra (je te recommande vivement ce logiciel gratuit pour la géométrie et la géométrie analytique) : il faut quand même beaucoup de patience, j'ai mis un "certain" temps pour la figure de 14 h 10.
Ensuite pour les poster sur le fond du forum j'enregistre dans le format .gif avec fond transparent. Je passe pour cela par un autre logiciel gratuit : MWSnap 3

C'est un peu toute une gymnastique ; mais le résultat en vaut la peine je crois.

Correction : la figure du cube a été faite avec Paint

Ok.

Je pense que je vais installer ce logiciel.
Comme ça, la prochaine fois sur des sujets comme celui là, je pourrai poster mes essais.

Si tu as Windows, alors tu as déjà Paint

Il est facile de trouver Geogebra

Un lien utile :

Oui, j'ai Paint. (mais je pense ça aurait été dur de faire la dernière figure avec)

Merci pour le lien.
J'espère que Geogebra n est pas trop dur à utiliser.

Geogebra est un logiciel qui demande des efforts. Mais tu peux progresser beaucoup en géométrie et géométrie analytique en l'utilisant régulièrement.

Je t'en prie et à une prochaine fois !