Inscription / Connexion Nouveau Sujet
pb sur les fonctions
g 1 exo à rendre en math et je ne comprend strictement rien
si qq'1 peut m'aider ce sera avec 1 grand merci
voici le pb :
etudiez les variations de la fonction f définie sur R par
f(x) = 5 ! x + 1 ! - 4 ! 3 - 5 ! (les ! ses sont des valeures absolues)
donner sa représentation graphique dans un repére (O,, i, j)
Salut,
Une petite question, tu écrit f(x) = 5 ! x + 1 ! - 4 ! 3 - 5 !, ne manque-t-il pas un x quelque part dans le dernier terme avec les valeurs absolues?
Nico
Bonjour veroc!
Je récris ta fonction car les ! signifient souvant autre chose et ça me trouble en tout cas.
Puis je me demande si c'est vraiment ça ou s'il y a une faute de frappe car |3-5|=|-2|=2 et dans ce cas la fonction vaut
Si c'est bien ça je regarderais séparément les cas x > 1, x < 1 et x = 1.
 Isis
Isis
g 1 exo à rendre en math et je ne comprend strictement rien
si qq'1 peut m'aider ce sera avec 1 grand merci
voici le pb :
etudiez les variations de la fonction f définie sur R par
f(x) = 5 ! x + 1 ! - 4 ! 3 - 5 x ! (les ! ses sont des valeures absolues)
donner sa représentation graphique dans un repére (O,, i, j)
>veroc
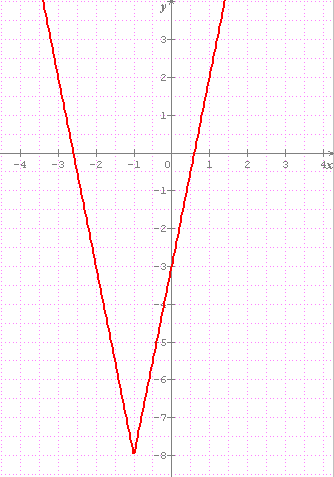
si c'est 5|x+1|-4|x-5|, tu dois trouver ça :
(explications de Isis)
vérifies ton énoncé
pour les valeurs absolues, plutôt que le point d'exclamation, fait AltGR 6 : |
Philoux
je récris la fonction :
f(x) = 5 | x + 1 | - 4 | 3 - 5 x |
g 1 exo à rendre en math et je ne comprend strictement rien
si qq'1 peut m'aider ce sera avec 1 grand merci
voici le pb :
etudiez les variations de la fonction f définie sur R par
f(x) = 5 |x+1| -4 |3-5x|
donner sa représentation graphique dans un repére (O,, i, j)
>veroc
As-tu vu les valeurs absolues en cours ?
Philoux
g 1 exo à rendre en math et je ne comprend strictement rien
si qq'1 peut m'aider ce sera avec 1 énorme grand merci
voici le pb :
etudiez les variations de la fonction f définie sur R par
f(x) = 5 |x+1| -4 |3-5x|
donner sa représentation graphique dans un repére (O, i, j)
*** message déplacé ***
comment ca
je sais qu'une valeure absolue est toujours positive
en fait je me suis dis que pour
5x + 5 > -12 + 20x on trouve la valeure où x est positif
5x + 5 < -12 + 20x on trouve la valeure où x est négatif
alors le résultat c 1,13
mais aprés je bloque
salut veroc 
en fait, il faut que tu fasses un tableau de signe ...
si x > -1 -> |x+1| = x+1
si x = -1 -> |x+1| = 0
si x < 1 -> |x+1| = -x-1
si x > 3/5 -> |3-5x| = -3+5x
si x = 3/5 -> |3-5x| = 0
si x < 3/5 -> |3-5x| = 3-5x
Voila. Reste plus qu'a faire le tableau ... 
dis nous si tu rencontres des difficultées !
lyonnais

de rien, mais j'aimerais bien une confirmation de la part de philoux ( j'ai peur de te dire des bétises  )
)
...
En lecture rapide, ça semble parfait lyonnais (avec beaucoup de pédagogie, en plus)
Philoux
La courbe complète, cette fois-ci, avec chgt d'échelles 
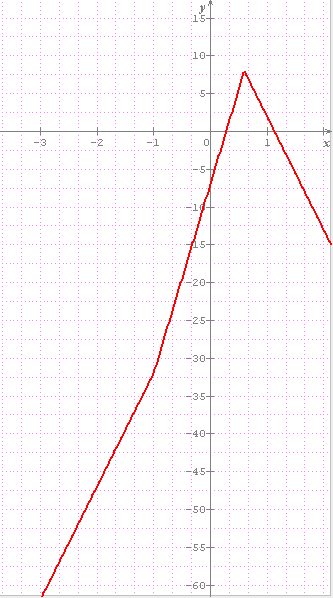
f(x)=5|x+1|-4|3-5x|
Df = R
sur ]-oo;-1[ f(x)=-5(x+1)-4(3-5x)=-5x-5-12+20x=15x-17
sur [-1;3/5[ f(x)=5(x+1)-4(3-5x)=5x+5-12+20x=25x-7
sur [3/5;+oo[ f(x)=5(x+1)+4(3-5x)=5x+5+12-20x=-25x
il faut étudier ces 3 fonctions sur leur intervalle
*** message déplacé ***
>pas de multi post veroc
Philoux
*** message déplacé ***
ah oui, escuse ...
pour obtenir 15x-17sur l'intervalle ] ;-1] ( corrige, dans le tableau j'ai fais une faute de frappe et j'ai mis 15x-18 ), il faut faire :
;-1] ( corrige, dans le tableau j'ai fais une faute de frappe et j'ai mis 15x-18 ), il faut faire :
et tu fais pareil pour les autres.
Mais t'as question s'est d'étudier le signe de g(x) ou quoi ?
pas passé
peut-être un crochet qui manque (t'as fait un delete ?)
Philoux
ok merci philoux 
j'ai du faire une fausse manip, je sais pas laquelle mais bon 
sinon, pour l'exo de veroc, après faut qu'elle étudie le signe de f(x) ou pas ?
il n'est demandé que la représentation graphique => segments de droites comme indiqué dans le graphe.
Philoux
bon ba alors je crois que l'on a fait le tour ... encore du bon travail d'effectuer !
PS : magnifiques tes courbes philoux 
@+ sur l'
lyonnais

>on peut continuer, un peu, lyonnais
discuter, selon fa valeur de m, le nombre et le signe des solutions de f(x)=m
Philoux
lyonnais ouh ouh !
Tu es tout à fait capable de résoudre ça !
Philoux
pour moi, voici les réponses ( rectifis si je me trompe ) :
si , il y a deux solutions.
si m = 8 , il y a une solution
si m > 8 il n'y a pas de solutions
T'as pas (complètement) répondu à la question !
Philoux
par ailleurs, ton tableau contient une autre faute ; f(-1)=-33 et f(3/5)=8 et non 0
Philoux
oups escuse, j'avais mal lu la question ( comme d'habitude  )
)
alors signe de f(x) = m
sur ]-\infty;0[ -> les deux solutions sont négatives
pour m = 0 -> les deux solutions sont sur l'axe des abscisses
sur ]0;8[ -> les deux solutions sont positives
pour x = 8 -> la solution est positive
C'est bon là ?
nan, mais dans mon tableau c'est pas 0 ...
enfin, j'ai mis ça pour dire qu'on changeais de fonction et en aucun cas de signe ... dsl si je me suis mal fais comprendre !
...