Inscription / Connexion Nouveau Sujet
point anguleux
bonjour, à un test mon prof me demande de définir un point anguleux. J'ai répondu:
point qui est défini et dont la dérivé à droite et à gauche est différente et non infinie.
il me la comptée fausse en barrant le non infinie et en soulignant le "qui est défini"
Pourriez vous m'éclairer sur ma faute car je ne comprends pas?
merci
merci, mais je devais donner une définition en français. Donc je ne vois toujours pas où est ma faute.
salut,
bah je pense que t'avais jute mal formulé parce que "non infini" et "qui est défini" c'est pareil il me semble...
après ca semble difficile a croire qu'il t'ait tout compté faux juste pour une formulation...
Salut,
lorsque la dérivée à droite et à gauche ne sont pas les mêmes alors il y a un point anguleux.
si je dis:
point d'une fonction définie et dont la dérivé à droite et à gauche est différente et pas infinie.
c'est bon? Car pour mon prof, il faut garder la notion d'appartenir au domaine de définition et de ne pas être infini.
Bonjour,
Quand tu dis
non infinie
Et il me semble que c'est bien ce que ça veut dire.
"non infini" est différent de "bien définie"
tout est dans la réponse de 12:10
voila comment j'aurais dit, et comme LeFou participe à la converse il me corrigera
Soit f une fonction et x0 un point adhérent au Df.
La fonction f est dite dérivable à droite (resp. à gauche) en x0.
si la lim respectivement à droite et a gauche donne un nombre fini différent
alors Cf admet un point anguleux (x0 ; f(x0))
Déjà, en 1ère S, on ne sait pas ce qu'est un point adhérent!
Moi j'aurais dit :
Un point anguleux () est caractérisé par des limites finies différentes à droite et à gauche, de plus la fonction en question admet une valeur exacte en
.
je suis en 5ème secondaire en Belgique et j'ai vu la notion de point adhérent, la définition de mdr_non de 15h50 me parait la mieux.
Merci beaucoup
Sauf que sa définition est fausse(sauf erreur de ma part) car la limite doit être la même à droite et à gauche .
Un point anguleux (x0) est caractérisé par des limites finies différentes à droite et à gauche, de plus la fonction en question admet une valeur exacte en x0.
Sauf que sa définition est fausse(sauf erreur de ma part) car la limite doit être la même à droite et à gauche .
j'ai peut etre (surement) mal compris ton message. Mais es ce que tu ne contredis pas ta déf de 16:30 ?
ah oui j'avais mal lu, toute facon, le point ne peut être défini si la limite à droite et à gauche est différente. Mais en fait je suis un peu troublé par vos termes car je n'ai pas appris de la même manière. (programme math forte belge)
donc je dirais:
Soit f une fonction et A un point adhérent au Df.
si la dérivé en A respectivement à droite et a gauche donne un nombre fini différent
alors A est un point anguleux (A ; f(A))
Bonjour,
Sans vouloir mettre de l'huile sur le feu, on pourrait très bien avoir une dérivée infinie dans le cas d'un point anguleux…
Voici une définition qui permettra probablement de mieux y voir clair .
Le graphique d'une fonction f présente en P(a ;f(a)) un point anguleux si f est continue en a et si les dérivées à droite et à gauche sont réelles mais ne sont pas égales ou si une seule de ces dérivées est réelle et que .
J'ai des doutes sur cette définition, car je vois dans ma tête des courbes comme une astroïde qui possède 4 points anguleux et dont deux ne respecte pas cette définition. ( Droite et gauche )
LeFou
Je retire ce que j'ai dit


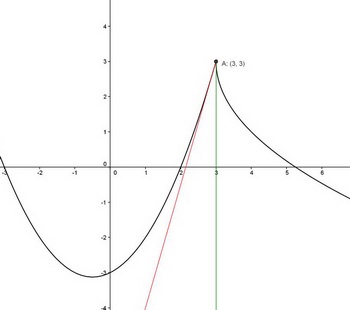
Le point A(3;3) ci-dessous est bien un point anguleux.
Ce que j'ai écrit signifie :
.
ou
.
ou
.
ou
.
Pour la fonction valeur absolue, il n'est pas du tout question de cela
Pour en revenir à la fonction f(x) = |x|, le graphique comprend un point anguleux A (0 ;0) car d'une part f est continue en 0, d'autre part f'(0-) = -1 et f'(0+) = +1.
Comme f'(0-) et f'(0+) sont deux nombres réels distincts, la définition de point anguleux s'applique en A.
C'est exact et pourtant cela ne correspond pas avec ta définition qui parle essentiellement de limites infinies non ?
Mais si elle correspond parfaitement à la définition (qui n'est pas la mienne mais qui est la définition classique...)
Tu as probablement mal lu cette définition.
Le graphique d'une fonction f présente en P(a ;f(a)) un point anguleux si f est continue en a et si les dérivées à droite et à gauche sont réelles mais ne sont pas égales si une seule de ces dérivées est réelle et que
.
Une disjonction de deux propositions étant vraie dès que l'une des deux propositions est vraie, dans le cas de la valeur absolue, la première partie de la définition est vérifiée.
Donc la définition est bien appliquée. 



