Inscription / Connexion Nouveau Sujet
point d'intersection
Bonjour, je suis bloqué à cet exo, pouvez-vous m'aider svp ?
On considère les droites d'équation
(d1) : 2x+3y-15=0
(d2): 5x-y+5=0
(d3): x+1.5y+2=0
(d4):y=5x-7
Déterminer le point d'intersection.
Voilà ce que j'ai fais :
J'ai mis (d4) sous la forme cartésienne et j'ai mis les même coefficient devant y :
On a (d4): -5+y+7=0
Le système à résoudre après avoir mis le coef devant y est :
2x+y=15
15x-3y=-15
2x+3y=-4
-15+3y=-21
Le problème c'est que quand je soustrais, toute les lignes, j'ai 0x et 0y= 55 :/
bonjour,
imaginons que tu n'aies que 2 droites d1 et d2 et tu dois trouver le point d'intersection.
on a le système
(d1) : 2x+3y-15=0
(d2): 5x-y+5=0
ou
système équivalent à si on multiple par 3 l'équation d2
Et additionnons
d1= 2x+3y-15
d2=15x-3y+15=0
---------------------------
d1+d2= 17x=0
x=0
trouvons y en remplaçant x par 0 dans une des équations
par exemple prenons d1
d1) : 2x+3y-15=0
3y-15=0
ou
y=15/3=5
bonjour : )
Penses-tu que deux droites parallèles peuvent se croiser ?
1) Regroupe les droites parellèles. Qu'obtiens-tu ?
2) Calcule les intersections entre un groupe de droite et l'autre.
Bonjour,
On a les 4 droites d'équations :
(d1): 2x+3y-15=0
(d2): 5x-y+5=0
(d3): x+1.5y+2=0
(d4): y=5x-7
Ces 4 droites définissent un quadrilatère.
Comme il y a qu'une équation réduite, je l'ai mis en cartésienne :
(d4): -5y+7=0
Puis après j'ai mis les lettres et les nombres d'un côté, puis le coefficient devant y.
Donc j'ai multiplier (d2) par 3; (d3) par 2 et (d4) par 3.
J'obtiens :
(d1): 2x+3y=15
(d2): 15x-3y= -15
(d3): 2x+3y=-4
(d4): -15x+3y=-21
En faisant (d1)-(d2)-(d3)-(d4), j'obtiens 0x et 0y pour 55
Je sais pas ou est mon erreur.
Et je ne pense pas que (d4) est parallèle à (d2) puisque ce sont les droites d'un quadrilatère.
Non.
Il y a plusieurs problèmes dans tes analyses.
*** Comme on a un quadrilatère tu penses que des droites ne peuvent être parellèles.
Un rectangle n'est-il pas un quadrilatère ?
*** *** Il est important de savoir reconnaitre des droites parellèles.
Soit (D1) : ax + by + c = 0 et (D2) : a'x + b'y + c' = 0.
(D1) et (D2) sont parallèles si ab' = a'b.
Ici il y en a des droites parallèles, suis donc mon premier message et indique nous les droites qui sont parallèles.
C'est bien.
On a deux groupes de droites qui sont parallèles (et non confondues) :
Groupe 1 : (d1) et (d3)
Groupe 2 : (d2) et (d4).
Il doit t'être bien clair maintenant que (d1) et (d3) n'ont aucun point en commun, et de même (d2) et (d4) n'ont aucun point en commun.
N'est-ce pas ?
Si tu es d'accord, on trouve au final quatre intersections possibles : lesquelles ?
Oui mais encore ?
(d1) et (d3) sont parallèles et disjointes, elles ne se croisent donc jamais (pour la même raison (d2) et (d4) ne se croisent jamais).
En revanche, (d1) et (d2) se croisent et (d1) et (d4) se croisent aussi.
De même (d3) et (d2) se croisent et (d3) et (d4) se croisent également.
Les voici les 4 intersections à chercher.
D'accord, donc je dois résoudre les système :
(d1): 2x+3y-15=0
(d2): 5x-y+5=0
(d1): 2x+3y-15=0
(d4): -5+y+7=0
(d3): x+1.5y+2=0
(d2): 5x-y+5=0
(d3): x+1.5y+2=0
(d4): -5+y+7=0
Il faut que je mette le même nombre devant y et que j'additionne c'est ça ?
(d1): 2x+3y-15=0
Il faut que je mette le même nombre devant y et que j'additionne c'est ça ?
Et la remarque de kenavo27 te permettra de visualiser que tout ça a un sens.
Avoir toujours un graphique sous la main quand c'est possible.
D'accord merci,
J'avais fait un graphique aussi 
Par exemple, pour le 1er système à résoudre
(d1) et (d2)
En multipliant (d2) par 3, pour avoir le même nbre devant y j'ai :
(d1): 2x+3y=15
(d2): 15x-3y=-15
-12x-6y=30
Est ce que j'ai bon ? svp
En multipliant (d2) par 3, pour avoir le même nbre devant y j'ai :
(d1): 2x+3y=15
(d2): 15x-3y=-15
Il est facile d'y remédier, comment ?
(d1):2x+3y=15
(d2):-15x+3y=15
donc
-17x+0y=0
donc y= 17 x
Je remplace y
(d1):2x+17x=15
18x=15
x=15/18
?
d1):2x+3y=15
(d2):-15x+3y=15
donc
-17x+0y=0
donc y= 17 x
donc -13x=0 ou x=0
et
si l'on remplace x par 0 dans 2x+3y =15(par exemple)
on obtient
3y=15
ou
y=5
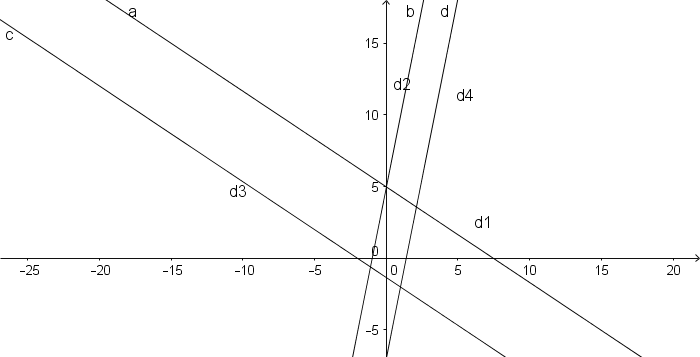
regarde le graphique, on a bien l'intersection (0;5)
D'accord merci pour beaucoup !
Pour (d1) et (d4)
J'obtiens
(d1):2x+3y-15=0
(d4):-15+3y+21=0
Donc -13x= ?
Je dois faire -15+21 ou -15-21 svp ?
Ah oui !
(d1): 2x+3y-15=0
(d4): y=5x-7
(d1): 2x+3y=15
(d4): -5x+y+7 =0 -> -5x+y=-7
(d1) : 2x+3y=15
(d4): -15x+3y=-21
c'est bon ça ?
Pour (d3) et (d2)
(d3) : x+1.5y+2=0
(d2): 5x-y+5=0
(d3): x+1.5y=-2
(d2): 5x-y=-5
(d3): x+1.5y=-2
(d2): -7.5x+1.5y=7.5
-6.5x= (-2-7.5) ou (-2+7.5) ?
Pour (d3) et (d4)
(d3): x+1.5+2=0
(d4): y=5x-7 -> -5x+y+7=0
(d3): x+1.5y=-2
(d4): -5x+y=-7
(d3): x+1.5y=-2
(d4): -7.5x+1.5y=-10.5
-6.5x= (-2-10.5) ou (-2+10.5) ?
Merci
(d3): x+1.5y+2=0
(d2): 5x-y+5=0
(d3): x+1.5y+2=0
d2: 5x-y+5=0
(d3): x+1.5y+2=0
d2: 7.5x-1.5y+7.5=0 (cette équation est obtenue en multipliant chaque terme par 1.5 la première équation d2 (d2: 5x-y+5=0)
----------------------------------
8.5x+9.5=0
x=-9.5/8.5
sauf erreur
tu as écrit ;
(d3): x+1.5y=-2
(d2): -7.5x+1.5y=7.5 tu remarqueras que tu ne peux riens éliminer ni les ni les y
D'accord merci,
donc je remplace x dans la première
(9.5/8)+1.5y+2=0
1.5y= (-9.5/8) -2
1.5y = -51/16
y= (-51/16)/1.5
y= -2.125
c'est bon ça pour (d3) (d2) ? svp
désolé c'est x= 9.5/8.5 donc
(9.5/8.5)+1.5y+2=0
1.5y=(-9.5/8.5)-2
1.5y=-53/17
y= (-53/17)/1.5
y= -106/51
c'est ça svp ?
School,
Tu as beaucoup de mal avec la résolution des systèmes de deux équations à deux inconnues.
La combinaison n'est pas la seule méthode, il existe également la substitution.
Pour la combaison, on n'est pas obligé de faire tous le temps 'équation 1' - 'équation 2'. On peut très bien faire 'équation 1' + 'équation 2'.
Le seul objectif est de faire disparaitre une inconnue.
*** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** ***
*** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** ***
Ton premier essai :
Par exemple, pour le 1er système à résoudre
(d1) et (d2)
En multipliant (d2) par 3, pour avoir le même nbre devant y j'ai :
(d1): 2x+3y=15
(d2): 15x-3y=-15
-12x-6y=30
Est ce que j'ai bon ? svp
Tu n'as pas bon (c'est -13x + 6y = 30) ; mais ça ne t'avance à rien car tu avais choisi de faire disparaitre l'inconnue y mais il est toujours là.
[ En faisant (d1) - (d2) (ou (d2) - (d1)) aucune chance de faire disparaitre y. ] Etait-il difficile de voir qu'en faisant (d1) + (d2) on obtient : 17x = 0 ?
Ensuite d'ici on aurait eu sans problème x = 0/17 = 0, ce qui permet de trouver y en remplaçant dans une des équations.
Par exemple (d1) : 3y = 15 d'où y = 15/3 = 5.
*** *** *** *** *** *** *** *** *** *** *** ***
Ton deuxième essai :
(d1):2x+3y=15
(d2):-15x+3y=15
donc
-17x+0y=0
donc y= 17 x
-17x + 0y = 0 est équivalente à -17x = 0
On trouvait alors à nouveau x = 0 ce qui permet de trouver y en remplaçant dans une des équations.
Par exemple (d1) : 3y = 15 d'où y = 15/3 = 5.
L'intersection de (d1) et (d2) est le point de coordonnées (0 , 5).
*** *** *** *** *** *** *** *** *** *** *** ***
Comment en être sûr ?
Ici on a deux façons de vérifier :
Premère façon : On revient au système du début et on remplace pour vérifier si ça marche.
On a trouvé x = 0 et y = 5 pour solution à :
(d1) : 2x + 3y - 15=0
(d2) : 5x - y + 5=0
Si on remplace dans (d1), on a 2*0 + 3*5 - 15 = 0 + 15 - 15 = 0 donc (d1) est vérifiée.
Si on remplace dans (d2), on a 5*0 - 5 + 5 = 0 donc (d2) est vérifiée.
Donc on a bon.
Deuxième façon : On observe sur le graphique que l'intersection de (d1) et (d2) est bien le point de coordonnées (0 , 5).
*** *** *** *** *** *** *** *** *** *** *** ***
kenavo27 avait déjà donné la réponse.
*** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** ***
*** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** *** ***
On poursuit :
Ah oui !
(d1): 2x+3y-15=0
(d4): y=5x-7
(d1): 2x+3y=15
(d4): -5x+y+7 =0 -> -5x+y=-7
(d1) : 2x+3y=15
(d4): -15x+3y=-21
c'est bon ça ?
Tu utilises la méthode de combinaison à nouveau. Mais tu pouvais sans problème utiliser la méthode de susbstitution.
On y = 5x - 7.
Donc si on substitue dans (d1) on obtient quoi ?
2x + 3(5x - 7) - 15 = 0
On a une équation à une inconnue et on peut trouver x.
Qu'on ait les résultats à un endroit :
L'intersection de (d1) et (d2) est le point de coordonnées (0 , 5).
L'intersection de (d1) et (d4) est le point de coordonnées (36/17 , 61/17).
L'intersection de (d3) et (d2) est le point de coordonnées (-19/17 , -10/17).
L'intersection de (d3) et (d4) est le point de coordonnées (1 , -2).
D'accord merci pour tout !
Mais pour (d1) et (d4)
On trouves bien
(d1): 2x+3y=15
(d4): -15+3y=-21
Comment vous avez trouver y=5x-7 ?
Comment vous avez trouver y=5x-7 ?
C'était déjà donné.
(d4):y=5x-7
Si tu veux. C'est la méthode de substitution.
***************************************************************
Les étapes sont :
Etape 1 :
Choisir une équation ;
ET
Exprimer une des inconnues en fonction de l'autre (dit autrement: isoler une des inconnues).
Etape 2 :
Prendre l'équation non utilisée à l'étape précédente ;
ET
A l'intérieur de celle-ci, remplacer l'inconnue précédemment isolée par l'expression obtenue.
Etape 3 :
Résoudre l'équation à une inconnue obtenue à la fin de l'étape 2.
Etape 4 :
Utiliser l'expression obtenue à l'étape 1 pour trouver la seconde inconnue.
Etape 5 :
Vérifier que cela fonctionne.
***************************************************************
***************************************************************
***************************************************************
En étape, on veut résoudre :
(d1) : 2x + 3y- 15 = 0
(d4) : y = 5x - 7
Etape 1 :
Je choisis (d4) et je choisis d'isoler la variable y. ((d4) donnait déjà la variable y en fonction de x donc il n'y a rien à faire.)
y = 5x - 7
Etape 2 :
L'équation non utilisée est (d1), on remplace y dedans.
2x + 3(5x - 7) - 15 = 0
Etape 3 :
On résout l'équation : 2x + 3(5x - 7) - 15 = 0
2x + 15x - 21 - 15 = 0
17x = 36
x = 36/17
Etape 4 :
Comme on a trouvé x, on remplace dans l'équation de l'étape 1 pour trouver y.
y = 5*36/17 - 7 = 61/17
Donc on trouve comme solution x = 36/17 et y = 61/17
Etape 5 :
On a des doutes parfois, alors on vérifie si on ne s'est pas trompé.
On doit vérifier si 2x + 3y- 15 = 0 et si y = 5x - 7
Pour la première : 2*36/17 + 3*61/17 - 15 = (72 + 183)/17 - 15 = 15 - 15 = 0 (c'est bon c'est vérifié).
Pour la deuxième : 5*36/17 - 7 = 61/17 (c'est bon c'est vérifié).
Conlusion : on trouve que le point d'intersection de (d1) et (d4) a pour coordonnées (36/17 , 61/17).
***************************************************************
***************************************************************
Tu peux essayer de reproduire pour (d3) et (d4).
Mais j ai pas compris pour d3 et d2 :/
(d2) : 5x - y + 5 = 0
(d3) : x + 1.5y + 2 = 0
Essaie d'utiliser la méthode par substitution que tu viens d'apprendre. Comme ça tu t'entraineras.
Je suis a (d3) et (d2) la^^
(D3): x+1,5y+2=0
(D2): 5x-y+5=0
En multipliant d2, par 1,5:
(D2): 7,5x -1,5y +7,5=0
C est un bon début ?
Par substitution pour d3:
On peut isoler x
x= -1,5y -2 ?
Fais ensuite par combinaison comme tu as commencé, et tu pourras comparer les résultats.
Je te corrigerai à la fin aussi.
Allez, je te laisse du temps, prends ton temps.
C est bon, j ai tout réussi !!! 
Je dois faire quoi avec les coordonnées des 4 points maintenant svp?
Je dois faire quoi avec les coordonnées des 4 points maintenant svp?
Tu as juste écrit qu'il fallai trouver les 4 points.
On considère les droites d'équation
(d1) : 2x+3y-15=0
(d2): 5x-y+5=0
(d3): x+1.5y+2=0
(d4):y=5x-7
Déterminer le point d'intersection.
Tu as les 4 points donc tu as terminé l'exercice. S'il y a une suite à l'énoncé tu dois l'écrire.