Inscription / Connexion Nouveau Sujet
point d'intersection de deux courbes
bonjour, j'ai un exercice à résoudre et je n'y arrive pas, pouvez-vous m'aider svp? voici l'énoncé :
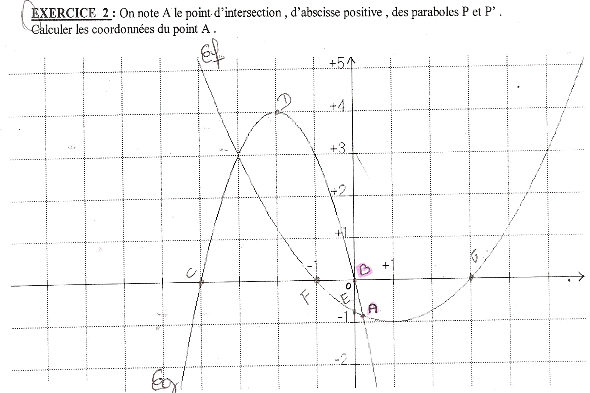
On note A le point d'intersection, d'abiscisse positive, des paraboles P et P'.
Calculer les coordonées du point A.
J'ai une figure avec deux courbes représentatives.
Je suis bloqué car je ne connais pas les fonctions, comment est ce que je peux faire?
Merci
Bonsoir laetitia,
Comme tu n'as pas les équations de paraboles, je pense qu'on veut une résolution graphique.
A moins que ...
Bonsoir,
Je crois que tu as une figure avec deux courbes qui se coupent deux fois, donc deux points d'intersection mais A est le point d'abiscisse positive ... une lecture graphique !
Soit tu peux faire une lecture graphique
Soit tu peux trouver pour chaque parabole 3 points qui vont te permettre de déterminer l'expression des fonctions représentées par ces paraboles
f(x) = ax2 + bx + c
avec 3 points de cette parabole tu dois pouvoir trouver a et b et c
g(x) = a'x2 + b'x + c'
avec 3 points de cette parabole tu dois pouvoir trouver a' et b' et c'
et pour trouver les coordonnées de l'intersection il faudra résoudre f(x) = g(x)
Salut Bourricot
Je lui conseille d'utiliser ta méthode s'il ne peut pas trouver les valeurs exactes des coordonées du point A Parce que si ça saute au yeux que A (1;2) je ne vois pas pourquoi il va chercher à compliquer Et ça dépond aussi de sa question, est ce qu'on lui demande une simple lecture graphique ou des calculs...
J'en doute qu'il a vraiment recopié son énoncé comme il l'a trouvé ..
T
désolé !
Ta méthode est plus juste
On saura peut-être un jour s'il faut calculer ou trouver graphiquement les coordonnées du point A !
Tous les espoirs sont permis 
Oui mais si elle a quelquchose dans le genre de la figure ci-desous .. il va bien falloir s'aider des points
A B et C
D E et F
pour touver l'expression de chaque fonction représentée
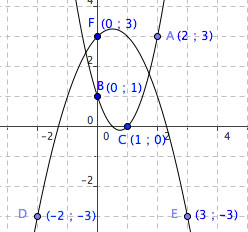
un petit détail : pas le point A, on le cherche déjà
Oui j'ai utilisé la même lettre A pour un point connu d'une des paraboles alors que cela devait être le point commun ...
Il faut donc se servir de L B et C
et D E et F ...
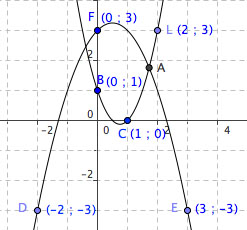
bonsoir Laetitia
les fonctions des paraboles sont de la forme ax²+bx+c
pour la première parabole
d'après le point B(0;1) : c = 1
d'après le point C(1;0) : a+b+c = 0; a+b = -c = -1; b = -a-1
d'après le point L(2;3) : 4a+2b+c = 3; 4a-2a-2+1 = 3; 2a = 3+2-1 = 4
a = 2; b = -2-1 = -3; la fonction est 2x²-3x+1
pour la deuxième parabole
d'après le point F(0;3): c = 3
d'après le point D(-2;-3) : 4a-2b+c = -3; 4a-2b = -3-c = -3-3 = -6; 2b = 4a+6; b = 2a+3
d'après le point E(3;-3) : 9a+3b+c = -3; 9a+6a+9+3 = -3; 15a = -3-9-3 = -15
a = -1; b = 2*-1 + 3 = 1; l'équation est -x²+x+3
2x²-3x+1 = -x²+x+3 -> 2x²-3x+1+x²-x-3 = 3x²-4x-2 = 0
x = 4
(16 +4*3*2))/6
j'ai essayer de m'aider de votre méthode mais je n'y arrive pas, je ne sais pas pourquoi!
je peux scanner mes paraboles?
oui, bien sûr, laetitia91
clique sur la mai
[lien]son
le sommet de Cg, concave, est D(-2;4) et celui de Cf, convexe, est H(1;-1)
toutes deux passent par I(-3;3)
c'est vrai mikayaou, mais c'est le point d'intersection d'abscisse positive, or le point I (-3;3) n'a pas d'abscisse positive
Je crois que mika t'a donné quelques points qui vont t'aider pour trouver A ..
oups.... mais je n'y arrive pas, j'ai pris trois points des paraboles et j'ai fait les équations et je dois surment me tromper car mon resultat est faux.
Bonjour laetitia91,
tu dois savoir que l'équation d'une parabole est de la forme y=ax²+bx+c
Prenons celle qui correspond à la fonction f. On a donc f(x)=ax²+bx+c
Tu dois savoir qu'on peut factoriser f sous la forme f(x)=a(x-x1)(x-x2), où x1 et x2 sont les 2 racines.
Pour f, on voit que les racines sont -4 et 0 donc f est de la forme:
f(x)=ax(x+4)
Voilà, il te reste à trouver le coefficient a.
Pour cela, tu peux par exemple utiliser le sommet de la parabole (-2;4), donc f(-2)=4
f(-2)=a*(-2)*(-2+4) = -4a = 4 donc a=1
Donc f(x)=-x(x+4) !
merci beaucoup jamo!
je pense pouvoir m'en sortir pour la deuxième =)
Ok.
Je pense que cette méthode est la plus simple, cela évite d'avoir à réoudre un système de 3 équations à 3 inconnues.
Avec ma méthode, une seule équation à 1 inconnue !
En effet mikayaou, c'est avec Géogébra que j'ai obtenu ces courbes.
Réponse un peu tardive ... mais en vacances je viens moins souvent
Annuler
connectez vous