Inscription / Connexion Nouveau Sujet
Points alignés.
Bonjour , j'ai besoin d'aide.
Merci d'avance.
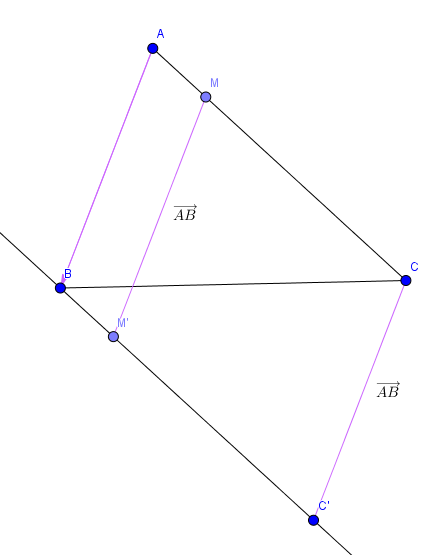
Soit ABC un triangle quelconque.M est un point quelconque de [AC].
M' est l'image de M par la translation de vecteur .
Démontrer que les points B, M' et C' sont alignés.
salut
tu peux exprimer les coordonnées des points de ta figure dans le repere R(A,AB,AC)
avec A(0,0) B(1,0) C(0,1) il te suffit d'ecrire les coordonnées de M,M' et C'
Bonjour
Mais c'est un peu lourd
AMM'B est un parallélogramme donc (BM') parallèle à (AC)
autant avec l'autre donc on a deux droites parallèles à une même troisième et elles ont un point commun
M ainsi n'est pas le translaté de M par la translation de
M' est tel que MABM' soit un parallélogramme
Ok ,
M' est tel que MABM' soit un parallélogramme
Pourquoi ?
M' est tel que MABM' soit un parallélogramme
Comment faites-vous pour savoir ?
A , M et C sont alignés ,
Or les points B , M' et C' sont les translatés respectifs des points A , M et C par
==> B,M' et C' sont alignés .
Merci beaucoup.
C'est une définition possible de la translation sinon vous avez .
Ceci définit bien un parallélogramme.
On en fait autant avec ACC' B qui est donc un parallélogramme donc
car toutes deux parallèles à (AC) ayant un point commun elles sont confondues
Autre possibilité L'image d'une droite par une translation est une droite parallèle L'image de (AC) est donc la droite passant par l'image de A c'est-à-dire B et l'image de C, C'.
M appartenant à (AC) son image M' appartient donc à (BC'). Les points B M' et C' sont donc alignés
Cela reprend un peu ce que vous vouliez dire mais la formulation me semble insuffisante