Inscription / Connexion Nouveau Sujet
Points d'intersections de deux fonctions
Bonjour.
J'ai longuement cherché sur le net une solution à mon problème, mais chaque réponse me semble illogique (et je finis toujours par bloquer).
Il m'est demandé de trouver via un calcul les deux points d'intersection de la fonction P(x) et de la droite d, en sachant que : P(x) = x² + x - 2 et d = 2x.
C'est certainement une question plutôt facile, mais là, je sèche complètement !
Je vous remercie d'avance pour votre précieuse aide 
Bonjour,
il s'agit plus exactement de trouver les points d'intersection de la courbe représentant la fonction P avec la droite (d) d'équation y = 2x
pour cela il te suffit de résoudre l'équation
pour visualiser ces points tu peux utiliser ta calculatrice graphique
représente la fonction P et la droite (d)
Lorsque l'on calcule un ou plusieurs points d'intersection, nous calculons la différence entre 2 fonctions :
Ici il suffit de faire la différence : P(x)- 2x
Tu auras ainsi une nouvelle fonction qui sera d'ailleurs polynôme.
Grâce aux notions du moment tu peux calculer : P(x) - 2x = 0
Avec ce calcul tu cherches les valeurs de x qui donnent les mêmes valeurs de y pour chaque fonction d'où 2 points d'intersections.
Lorsque tu auras ces 2 valeurs de x, tu pourras en calculer y et ainsi avoir tes 2 points d'intersections de coordonnées (x;y)
Bonjour.
Si deux courbes se coupent en un point cela signifie qu'elles y ont mêmes abscisses et mêmes ordonnées.
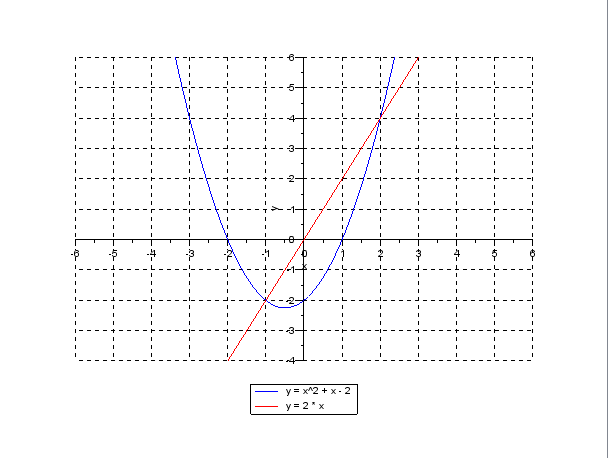
Un exemple avec le graphique ci-dessous.
Si elles ont mêmes ordonnées alors dans ton cas P(x) = d(x).
La résolution de l'équation P(x) - d(x) = 0 te donnera l'abscisse du point d'intersection.
A+