soit f(x) = ax² + bx + c dans le repère (B ; BA ; BD)
avec a négatif car la parabole est tournée vers le bas.

f(0) = 5
f(3) = 0
f'(t) = 2at + b = 0  avec f(t) = 9

Dans l'exercice, on cherche t

Matheuse23 devra dire si il (elle) a déjà étudié les dérivées....en début de 1re, peut-être un peu juste...

oui, oui.
Sinon ce sera la condition : sommet de la parabole en -b/2a

Merci beaucoup. Je n'ai pas encore étudié les dérivés.
F(x)= ax(carré) +bx + 5
Je vois pas ce que je dois faire Apres je suis désolée  

Bonjour,

Mettre ton expression sous forme canonique.

Bonjour
Oui ca fait
a(x+b/2a)carré - [b(carre)-20a]/4a

Je trouve ax(carré) +bx-5a donc La fonction est -x(carré) +bx +5 ?

Euh je crois que c'est faux, j'ai continué et en fait ca me fait un truc bizarre.

je te donne un lien, qui n'est pas le même exo, pas posé pareil, etc...mais qui devrait te faire comprendre ce qui se passe...et ainsi te mettre sur la voie Fonction polynôme du second degrès sauterelle

J'arrive à rien.
-a(x+b/2a)carré +9

Sais-tu au moins ce que tu cherches ?

Bah si j'avais a ou b ce serait bien je pense mais nan je comprends rien à cet exercice meme en Le retournant dans tout les sens

Je cherche -b/2a pour le sommet

Reprenons :
Enoncé
Une sauterelle saute d'un mur et on considère que sa trajectoire suit un arc de parabole.

Je pense qu'une sauterelle tu sais ce que c'est ;D, donc c'est quoi une parabole ?

Reprenons :
Enoncé
Une sauterelle saute d'un mur et on considère que sa trajectoire suit un arc de parabole.

Je pense qu'une sauterelle tu sais ce que c'est , donc c'est quoi une parabole ?

Bah c'est une courbe qui définit graphiquement la fonction polynôme du second degré

Et ça s'écrit sous quelle forme cette affaire là ?

Bah ax[sup][/sup]+bx + c

Ax² +bx+c

Hum ou a(x+b/2a)² - b²+4ac /4a

Non.

Je réitère ma question autrement.

Nous avons affaire là à une parabole, d'où ma question : sous quelle forme s'écrit l'équation d'une parabole ?

Bah je sais pas moi y a trois formes La forme canonique, formé développée et factoriser avec a(x-x₁)(x-x₂)

Tu ne réponds pas à ma question si ce n'est de me dire que tu ne sais pas.

Je me permets, sans vouloir t'embêter, de te la reposer, car c'est du cours : sous quelle forme s'écrit l'équation d'une parabole ?

F : x -> ax² + bx + c
Svp aidez moi j'arrive vraiment pas

Ce que tu m'as mis n'est pas une équation.

Ma question :  sous quelle forme s'écrit l'équation d'une parabole ?

La réponse attendue (que l'on trouve n'importe où sur google par exemple ...) :

Il suffit de taper dans google "Équation d'une parabole", prendre le premier site présenté, à savoir :
https://www.mathematiquesfaciles.com/paraboles_2_93254.htm
et dès la 2ème ligne du site c'est indiqué ...

Il suffit de taper dans google "Équation d'une parabole", prendre le premier site présenté, à savoir :
https://www.mathematiquesfaciles.com/paraboles_2_93254.htm ==>
et dès la 2ème ligne du site c'est indiqué ...

Oui pardon je sais ca mais je vois pas comment ca peut aider

Tu sais cela mais tu n'avais pas répondu à ma question ...
Donc je t'ai demandé quelque chose que tu sais, et tu n'as pas su me répondre.
Cela pose question, non ?

Oui bah je m'excuse.
Donc l'équation parabole est f(x) =ax²+bx +c avec a, b c appartiennent a R

Donc f(0)=5 donc c=5 (ça j'avais deja)
F(3) =0 donc f(3)= 9a+3b+5 =0
Et 9 La hauteur maximale tel que 9= -b/2a

Es-tu bien certaine de

Bah eu y = -b/2a ?
Sinon = 9 et = -b/2a

PS = je ne vois pas quelle relation je peux faire avec la hauteur maximale

f(-b/2a) = 9

Tu fais la même erreur depuis le début. Pas de violence, c'est le week-end !

Faisons une petite parenthèse :

L'équation d'une parabole s'écrit sous la forme suivante :



et l'on a :



L'extremum de ta parabole est tel que a pour coordonnées :

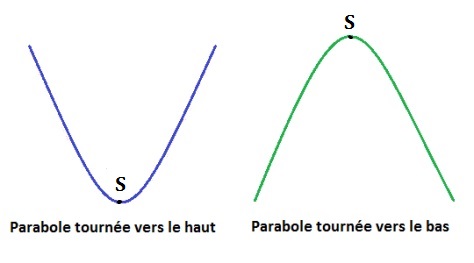
. si , ( positif, soyons positif (imagine la forme des lèvres quand on sourit) alors sourions , la courbe est tournée vers le haut : courbe bleue ci-dessous), ton extremum est donc un minimum (la valeur minimale que peut atteindre)

. si , ( négatif, nous sommes négatifs, tristes (imagine la forme des lèvres quand on est triste) ,  la courbe est tournée vers le bas : courbe verte ci-dessous) , ton extremum est donc un maximum (la valeur maximale que peut atteindre)

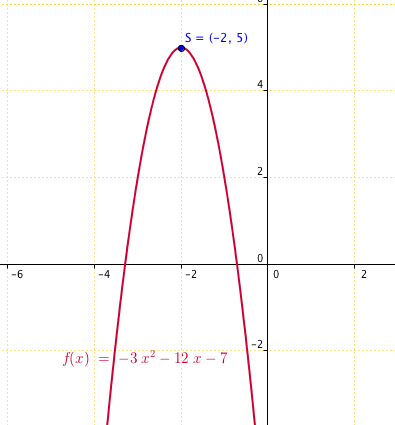
Exemple :



Tu as , négatif (triste ), ta courbe sera donc tournée vers le bas, tu auras donc un maximum pour

Merci à vous tous mais j'ai trouvé toute seule finalement.

Il faut résoudre le système :
9a+3b+5=0
-b²-20a /4a =9

On trouve b=20/3 et a=-25/9
Plus qu'à résoudre -b/2a et c'est dans la poche.
Bonne soirée à tous

Bonne soirée.

Bonjour,
Matheuse23 pourrais tu me dire comment tu en viens a ton systeme d'équation stp j'ai le meme exo que toi mais j'aimerais comprendre comment tu as fais

je comprend la premiere equation qui est dans ton systeme mais jsp comment tu as trouve la deuxieme