Bonsoir Serine

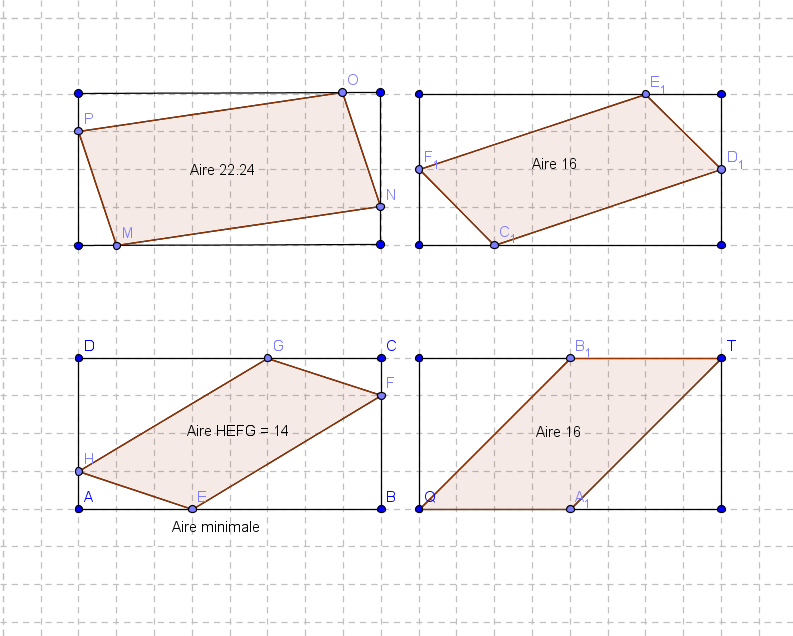
Tu peux calculer l'aire de MNPQ par différence entre l'aire de ABCD et les aires des triangles AMQ , BMN , CNP et PDQ . Inspire toi du schéma joint

L'aire de MNPQ sera une fonction du second degré en x contenant a .

La valeur qui annule la dérivée ( cette valeur est fonction de a ) donnera le minimum pour l'aire

okey, merci beaucoup de m'avoir répondu, c'est gentille

d'après ce que j'ai compris, il faut calculer l'aire du rectangle ABCD puis en soustraire l'aire des 4 triangle AMQ , BMN , CNP et PDQ.

c'est bien ça??

par contre je n'ai pas très bien compris ce que vous voulez dire par:
" La valeur qui annule la dérivée ( cette valeur est fonction de a ) donnera le minimum pour l'aire":?

merci d'avance et bonne soirée!

au faite, merci pour le schéma!!

Vous n'avez pas fait le chapitre des dérivées ?

Non pas encore!

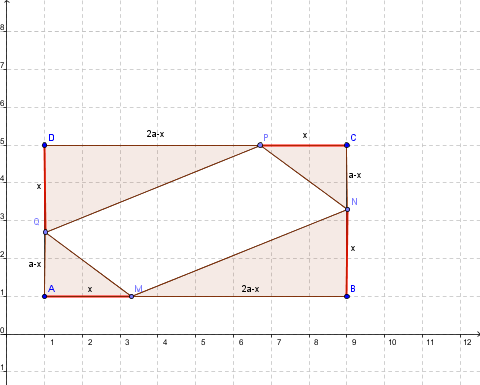
On va exprimer l'aire de MNPQ en fonction de x

aire de ABCD  : a*2a = 2a²

aire de AMQ + aire de CPN = 2*x(a-x)/2 = -x²+ax

aire de BMN + aire de PDQ = 2*x(2a-x)/2 = -x²+2ax

Aire de MNPQ  2a² -(-x²+ax)-(-x²+2ax) = 2x²-3ax + 2a²

Cette relation du second degré est une parabole dont vous avez certainement étudié le minimum ou le maximum .Si l'expression de la parabole est ax² + bx + c , on sait que le minimum (quand a est positif) est obtenu pour x = -b/(2a)


Ici , minimum pour x = -(-3a)/(2*2)= (3/4)a

Encore des illustrations

ahh d'accord, oui en fait j'avais commencé comme sa!
sérieusement, merci beaucoup de m'avoire aidée, c'est trés gentille

et merci encore pour les illustration!!

mais si sa ne vous dérange pas, il ya aussi un autre exercices que je comprend pas, ce n'est pas que je veux les réponce ou quoi, mais je ne comprend vraiment pas

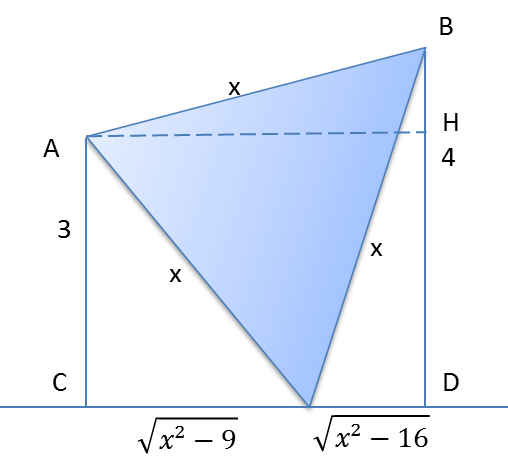
un drapeau a la forme d'un triangle équilatéral. il est suspendu par deux de ses coins au sommet de mâts verticaux de 3 et 4 métre de haut. le 3éme coin affleure exactement au sol. quelle est la longueur du côté de ce drapeau?

je ne vois pas vraiment comment faire ressortir une polynôme du second degré.
en tout cas merci beaucoup

j'ai pensé aux systhémes d'équation? est ce bon ou pas??

Bof.
Regarde ce dessin et dis-moi s'il t'inspire ? C'est plutôt Pythagore à tour de bras qu'il faut utiliser.

oui, en fait j'avais pensé à pythagore au début, mais il manque pas une inconnu,?

Pythagore dans AHB :
une équation, avec une inconnue x, je ne vois pas trop ce qui manque ?

ahh oui, autant pour moi!!
en fait il faut calculer les 3 longueur avec Pythagore, et après calculer les inconnus avec Pythagore isolé.
merci encore pour votre aide.