bonsoir
calculer la différence , voir quand cela est égal à 0, qui permettra de factoriser l'expression, dans le but de factoriser l'expression pour en étudier son signe

hum...c'est quoi les coordonnées de tes deux points A et B
parce que j'ai plus qu'un doute....pas d'intersection d'abscisse positive pour ces 2 fonctions...donne un peu un énoncé exact

J'ai pas les coordonnées de À et B . Mais j'ai y avec l'équation et je ne sais pas quoi faire avec.

Je pense c'est d'apres le graphique

eh beh...non, apparemment pas d'erreur
donc tu vas poser g(x)=f(x)-(5x-22)

et puis il va falloir étudier le signe de cette quantité

Je trouve pour x1 : -3,38 et x2: 1.3804 je sais si c'est correct

c'est quoi ces 2 valeurs ??
comment tu as trouvé ça ?

J'ai calculer comme vous l'a dit g(x)=f(x)-(5-22) et j'ai trouvé 3x²+6x-14 donc j'ai calculé les deux racines pour le polynôme du second degré. J'ai trouvé x1 et x2

euh ...g(x) est un polynôme de degré 3 et non 2

c'est la dérivée dont tu me parles là....
signe de la dérivée donc, avec des valeurs exactes (je crois que tu vas en avoir besoin ! ), du signe de la dérivée tu vas en déduire si g(x) s'annule ou pas entre 0 et 2....

Désole mais j'ai pas compris et je pense que je suis un confuse

salut,
refais le calcul de g(x)
puis etudie les variations de g

Je trouve x³+3x²-14x-11

Nn je me suis trompé c'est x³+3x²-14x+11

oui, mais écris des égalités, tu vas encore te perdre

g(x)= x³+3x²-14x+11 OK, donc ça, c'est l'expression de f(x)-(5x-22)

et maintenant dérive g etc....pour étudier les variations de g

Pour g'(x)= 3x²+6x -14 et les racines je trouve x1=-3,38 et x2=1,3804

garde sous le coude les valeurs exactes, au moins la positive, car tu vas en avoir besoin pour calculer son image par g ...et il faudra de la précision !

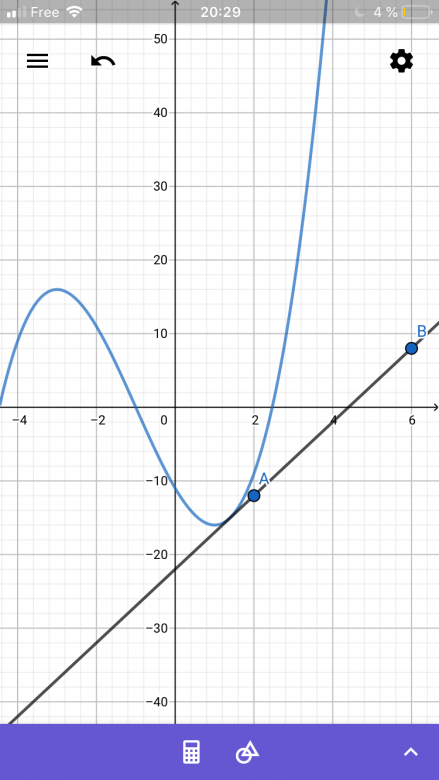
comme vous me l'aviez dit j'ai calculé son image par g. Je trouve 53,9787 pour le x1 et 0,0212 pour x2

ok
construis ton tableau de variations pour g
tu vas en déduire le signe de g(x)

Comment on construit un tableau pour g?

ben comme d'habitude !
signe de la dérivée donc de g'(x)
et variations de g en dessous

Est-ce correct ce tableau?

A comparer avec:

Je comprend pas ce qui faut comparer

non non pas de souci a priori
maintenant tu peux connaître le signe de g(x)
dans ton énoncé on te donnait un intervalle où tu étudiais ça, ou bien c'est sur R ?

c'est R, c'est bien ça: si  x appartient ]- infinie ; 53,978] g(x) > f(x) et si x appartient [0,0212;+infinie[ f(x)>g(x)

tu confonds x et y
g s'annule une fois

un peu d'aide