Bonjour .
j'ai un exercie à faire que j'aimerais que vous me corrigez .

Soit f la fonction définie sur I=[1/4;4] par f(x)=1/(3(x)) .

1.Montrer que f est une densité de probabilité .
2.Dans une population , le temps exprimé en heures passé quotidiennement par une personne devant un écran peut être assimilé à une variable aléatoire X dont la loi de probabilité a pour densité la fonction f définie dans la question 1.
Quelle est à 10^-3 près , la probabilité pour qu'une personne choisie au hasard dans cette population :
a. passe moins de 2 heures par jour devant un écran ?
b.passe plus d'une heure par jour devant un écran ?
3.a. Soit k . Soit G la fonction définie sur I par G(x)=kx(x) .
Déterminer le réel k pour que G soit une primitive de la fonction racine carrée sur I .
b. Calculer le temps moyen passé devant un écran par une personne de cette population .


1. f est dérivable sur I donc f est continue sur I .
_0,25⁴ f(x) dx = 1 donc f est une densité de probabilité .

2.a. P(X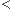2)61% . ( on intègre f(x) sur [1/4;2] ) .
b. P(X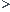1)66% . ( On intègre f(x) sur [1;4] ) .

3.a. on calcule G'(x) . on obtient: K(2(x))  et on peut donc en déduire que K=1/2 .

4. E(X) 1H18min .

merci d'avance .